
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ОСНОВНЫЕ ПРИЕМЫ ИЗУЧЕНИЯ ВЗАИМОСВЯЗЕЙ
Для исследования выявления наличия связи и дальнейшего изучения используется ряд различных специфических методов: элементарные (сопоставление параллельных рядов; построение корреляционной таблицы; графическое изображение) и более сложные (аналитических группировок, корреляционный и регрессионный анализ и некоторые непараметрические методы).
Метод сопоставления параллельных рядов является одним из простейших методов. Для этого факторы, характеризующие результативный признак располагают в возрастающем или убывающем порядке (в зависимости от эволюции процесса и цели исследования), а затем прослеживают изменение величины результативного признака. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяют установить наличие связи и ее направление. Зависимость между факторами и показателями может прослеживаться во времени (параллельные динамические ряды).
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
 |
│►1. Упорядоченные в табл. 1 данные при сопоставлении свидетельствуют о наличии обратной связи между себестоимостью и объёмом производства продукции.
Таблица 1
Производство и себестоимость продукции промышленного предприятия
| Пред-приятие | Произведено, тыс.т | Себесто-имость 1 т, руб. | Пред-приятие | Произведено, тыс.т | Себесто-имость 1 т, руб. |
| 7,0 | 10, | ||||
| 7,2 | 10,5 | ||||
| 8,3 | 11,2 | ||||
| 9,1 | 13,8 | ||||
| 9,5 | 14,0 |
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Первые попытки установления объективной меры взаимозависимости между признаками предпринимал Г Фехнер в конце XIX века. До сих пор используют дополнительные расчёты к данному простому методу с целью более объективного измерения тесноты корреляционной связи между факторным и результативными признаками (например, вычисление коэффициентов Фехнера – линейного коэффициента корреляции рангов или коэффициента конкордации Кэндела и Смита).
Балансовый метод заключается в том, что, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются так, чтобы итоги между отдельными частями были равны, т.е. чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения и т.п. Почти все народохозяйственные связи выражаются в виде балансов. Отчётный баланс народного хозяйства представляет собой сложную систему взаимосвязанных балансовых таблиц, правила их построения приведены в курсе экономической статистики.
Построение корреляционной таблицы проводится по результатам группировки. Они особым образом оформляются в виде корреляционной таблицы или решетки.
Корреляционная решетка представляет собой комбинационную таблицу, в подлежащем которой располагаются значения одного признака, как правило, факторного, а в сказуемом — другого, результативного. В клетках, образовавшихся при пересечении строк и граф, указываются частоты, т. е. число случаев, в которых одни значения сочетаются с другими.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
 |
│►2. По данным о количестве внесенных удобрений и урожайности картофеля по 60 хозяйствам области, приведенным в табл.2, проведены статистические исследования с использованием приёма построения корреляционной решётки для установления связи между количеством внесенных удобрений (х) и урожайностью посевов (у).
Таблица 2
Количество внесенных удобрений и урожайность картофеля по 60 хозяйствам области
Составим корреляционную таблицу зависимости урожайности от количества внесенных удобрений (табл.3). Таблица 3 Корреляционная таблица (Зависимость урожайности от количества внесенных удобрений)
Цифры, стоящие на пересечении строк и граф, показывают количество хозяйств с данным количеством внесенных удобрений и урожайностью. По корреляционной таблице можно сделать выводы о форме и направлении связи, а также о степени её тесноты. Если значения х и у расположены в возрастающем порядке и частоты сосредоточены около диагонали таблицы, идущей с левого верхнего угла в правый нижний, то этот свидетельствует о прямой связи между изучаемыми признаками, а с правого верхнего угла в левый нижний – об обратной связи. Причем связь будет тем теснее, чем плотнее концентрируются частоты у диагонали. Если частоты расположены по всей таблице равномерно, то это говорит о слабой связи или об отсутствии её между признаками. ◄
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Графический метод является очень удобным для визуальной оценки связи.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

 │►3. Данные предыдущего примера изобразим графически. Для этого результаты группировки единиц совокупности по факторному признаку и средние значения результативного признака по каждой группе нанесём на график в виде ломаной линии (рис. 1)
│►3. Данные предыдущего примера изобразим графически. Для этого результаты группировки единиц совокупности по факторному признаку и средние значения результативного признака по каждой группе нанесём на график в виде ломаной линии (рис. 1)
| Урожайность, ц/га |
Y
Х
| до 50 | 50-75 | 75-100 | 100-125 | 125-150 | 150 и выше |
| Внесено удобрений, кг/га |
Рис.1. Зависимость между урожайностью и удобряемостью
Средние значения результативного признака 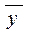 содержатся в последней графе табл.2). Полученная ломаная линия называется эмпирической линией регрессии. ◄
содержатся в последней графе табл.2). Полученная ломаная линия называется эмпирической линией регрессии. ◄
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Метод аналитических группировок также широко используется для изучения и измерения взаимосвязей социально-экономических явлений. Аналитические группировки позволяют установить наличие связи между двумя и более признаками и их направление. Метод группировок сочетается с методом средних и относительных величин. Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака.
Сопоставляя затем изменения результативного признака по мере изменения факторного можно выявить направление, характер и наличие тесноты связи между ними.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

│►4. По двадцати предприятиям области были установлены затраты на рекламу и количество оптовых покупателей, которые заключили договорные отношения благодаря информации из рекламной кампании. В табл.4 приведены данные о предприятиях, проранжированнные по величине затрат на рекламу.
Таблица 4
Ранжирование предприятий по затратам на рекламную кампанию
| Номер предприятия | Затраты на рекламную кампанию | Число оптовых покупателей продукции |
 Все наблюдения разбиты на группы в зависимости от величины признака – фактора (затраты на рекламу) и по каждой группе вычислены средние значения результативного признака (среднее число оптовых покупателей продукции) (табл.5).
Все наблюдения разбиты на группы в зависимости от величины признака – фактора (затраты на рекламу) и по каждой группе вычислены средние значения результативного признака (среднее число оптовых покупателей продукции) (табл.5).
Таблица 5
Результаты аналитической группировки
| Группы предприятий по затратам на рекламу | Число предприятий в группе | Среднее число оптовых покупателей продукции |
| Итого | - |
Сравнив средние значения результативного признака по группам, можно сделать вывод о том, что рост затрат на рекламу влечёт за собой увеличение числа оптовых фирм, заключивших договоры на поставку продукции предприятий. Таким образом, можно предположить наличие взаимосвязи между рассматриваемыми явлениями. Если бы связи между факторными и результативными признаками не было, то все групповые средние были бы одинаковыми по величине. ◄
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Корреляционная зависимость чётко можно обнаружить только при рассмотрении средних значений результативного признака, соответствующих определённым значениям факторного признака, так как при достаточно большом числе наблюдений в каждой группе влияние прочих случайных факторов взаимопогашается. Поэтому более чётко проявляется зависимость результативного признака от фактора, положенного в основу группировки.
Предполагается, что все прочие причины, если они носят случайный характер, при определении средней по группам взаимоугасают, т.е. дают в каждой группе один и тот же результат. Следовательно, различия в величине средних будут связаны только с различиями в величине данного факторного признака.
РЕЗЮМЕ
Все групповые средние примерно одинаковы по величине при отсутствии связи. Одним из недостатков аналитической группировки является неоднозначность результатов, которые зависят как от числа выделяемых групп, так и от установления границ интервалов. Аналитические группировки при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного или корреляционного анализов.
Дисперсионный анализ даёт возможность определить роли составляющих в общей вариации признаков, что позволяет по этой характеристике изменчивости судить о наличии связи между факторным и результативным признаком. Дисперсионный анализ не только позволяет определить роли случайных и систематических вариаций в общей, но и оценить достоверность полученных вариаций. Более подробно вопросы применения дисперсионного анализа будут рассмотрены в гл.3.
Корреляционный анализ и его задачи заключаются в том, чтобы измерить тесноту связи между варьирующими признаками, а также определить неизвестные причинные связи и оценить факторы, оказывающие наибольшее влияние на вариацию результативного признака. Подробнее о вопросах применения корреляционного анализа изложено в гл.2.
В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.
|

| v Общее понятие о видах, формах взаимосвязей. |
v Описание функциональных, стохастических и корреляционных связей.
v Этапы и основные приёмы изучения взаимосвязей.

|
Дата добавления: 2014-12-23; просмотров: 420; Мы поможем в написании вашей работы!; Нарушение авторских прав |