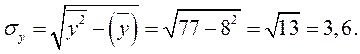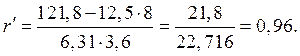КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рассмотрим использование парных коэффициентов корреляции для измерения многофакторной связи
Так, для измерения тесноты связи между двумя из рассматриваемых переменных можно применять парные коэффициенты корреляции.
Методика расчета таких коэффициентов и их интерпретация аналогичны методике расчета линейного коэффициента корреляции в случае однофакторной связи. Если известны средние квадратические отклонения анализируемых величин, то парные коэффициенты корреляции для примера из табл. 4 можно рассчитать проще, с использованием зависимостей
 (11)
(11)
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►5. По десяти предприятиям одной отрасли имеются данные о выпуске продукции (x) в тыс. ед. и о расходе условного топлива (y) в тоннах (графы 1 и 2 табл. 6).
Стоит задача найти зависимость расхода топлива от выпуска продукции (или уравнение регрессии y по x) и измерить тесноту зависимости между ними.
Таблица 6
Выпуск продукции и расход условного топлива на предприятиях
Предполагая линейную связь между параметрами уравнения регрессии, определим их значения из системы нормальных уравнений:
Все необходимые вычисления выполнены в табличной форме (табл. 3). В результате решения системы получим уравнение тренда в виде.
Отсюда Подставляя в это уравнение последовательно значения х=5,6,8,10 и т.д., получаем выравненные (теоретические) значения результативного показателя Для измерения тесноты связи между параметрами х и у воспользуемся линейным коэффициентом корреляции Так, используя зависимость (11), находим Определяем
Отсюда Значения линейного коэффициента корреляции r = 0,96 (близкого к единице) характеризует не только меру тесноты зависимости вариации у от вариации х, но и степень близости к линейной. ◄ |
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Корреляционный анализ позволяет при расчете определённых показателей выявлять степень влияния каждого из включенного в модель факторов на полученный результативный показатель при неизменном состоянии других факторов.
Частные коэффициенты корреляции применяются для необходимой проверки предположения о том, что связь между двумя переменными X и Y не зависит от влияния третьей переменной. В реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключения влияния двух переменных – второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.
Частный коэффициент корреляции первого порядка между признаками х1 и у при исключении влияния признака х2 вычисляют по формуле:
 . (12)
. (12)
По аналогии – для зависимости у от х2 при исключении влияния х1:
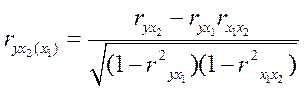 . (13)
. (13)
Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака:
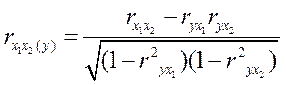 , (14)
, (14)
где rхiуi – парные коэффициенты корреляции между соответствующими признаками.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►6. Выполним расчет частных коэффициентов корреляции для нашего примера:
 ; ;  ; ;
 .
Итак, связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов слабее.
Практически отсутствует связь между факторными признаками при элиминировании результативного показателя .
Итак, связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов слабее.
Практически отсутствует связь между факторными признаками при элиминировании результативного показателя  . Это вполне понятно, внутрисменные простои и квалификация рабочих никак не связаны между собой (если не принимать во внимание необходимость выполнения задания). Другое дело, если стоит вопрос о выполнении задания: более квалифицированный рабочий допустит меньше внутрисменных простоев. Значение парного коэффициента корреляции, в этом случае . Это вполне понятно, внутрисменные простои и квалификация рабочих никак не связаны между собой (если не принимать во внимание необходимость выполнения задания). Другое дело, если стоит вопрос о выполнении задания: более квалифицированный рабочий допустит меньше внутрисменных простоев. Значение парного коэффициента корреляции, в этом случае 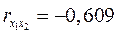 , подтверждает наличие довольно заметной обратной связи между этими факторами. Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы. ◄ , подтверждает наличие довольно заметной обратной связи между этими факторами. Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы. ◄
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
На основе парных коэффициентов корреляции и средних квадратических отклонений можно легко рассчитать параметры уравнения линейной двухфакторной связи

по следующим формулам:
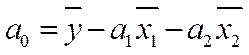 , (15)
, (15)
 (16)
(16)
 (17)
(17)
Показателем тесноты связи, устанавливаемой между результативными и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции  . В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:
. В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:
 (18)
(18)
где r – линейные коэффициенты корреляции (парные); подстрочные индексы показывают, какими признаками они исчисляются.
Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах -1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь является более интенсивной, а, следовательно, значение R ближе к единице.
Величина R2 называется совокупным коэффициентом множественной детерминации. Она показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение регрессии.
Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому, чем ближе R2 к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.
Многофакторный корреляционный анализ может быть использован в экономико-статистических исследованиях:
- для приближенной оценки фактического и заданного уровней;
- выявления резервов производства;
- краткосрочного прогнозирования развития производства.
Дата добавления: 2014-12-23; просмотров: 406; Мы поможем в написании вашей работы!; Нарушение авторских прав |



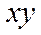
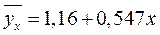




 (графа 5 табл.6).
(графа 5 табл.6).

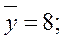

 и
и 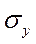 , предварительно найдя
, предварительно найдя  и
и