Оценим возможности использования коэффициента корреляции рангов Кендэлла

Ранговую корреляцию можно измерить с помощью коэффициента Кендэлла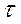

. (24)

Для нахождения величины S надо упорядочить по возрастанию ряд рангов переменной х. Затем рассматривается последовательность рангов переменной у. Для каждого наблюдения подсчитывается Р - число случаев, когда ранг признака у последующих наблюдений меньше, чем у данного, и Q-число случаев, когда ранг у следующих наблюдений больше, чем у данного. Искомое значение S:

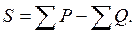(25)

Слагаемое Р рассматривать как меру соответствия последовательности рангов переменной у последовательности рангов переменных х. Слагаемое Q характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х.

Коэффициент Кендэлла изменяется в пределах от -1 до +1 и равен 0 при отсутствии связи между рядами рангов.

При наличии связанных рангов необходимо использовать скорректированную формулу коэффициента корреляции рангов Кендэлла. Пусть определяется теснота связи между k-м l-м признаками, в рядах значений которых имеются соответственно q и g групп объединенных рангов. Скорректированная формула для вычислений коэффициента корреляции рангов Кендэлла имеет вид:

, (26)

где , (27)

, (28)

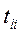, - число единиц в i-й группе объединенных рангов соответствующего признака.

Оценка статистической значимости коэффициента корреляции рангов Кендэлла проводится для больших значений n. Полученное значение коэффициента корреляции рангов сравнивается с величиной

, (29)

где - табличное значение нормального распределения для заданного уровня значимости α.

Если > ,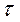

то гипотеза об отсутствии связи отклоняется на заданном уровне значимости.

При достаточно большем числе наблюдений между коэффициентами корреляции рангов Спирмэна и коэффициентом корреляции рангов Кендэлла должно выполняться следующее соотношение: . (30)

▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲