
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
АНАЛИЗА
Дисперсионный анализ (от латинского Dispersio – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике, медицине и др.
Целью дисперсионного анализа является проверка значимости различия между средними характеристиками с помощью сравнения дисперсий.
Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
Иногда дисперсионный анализ применяется, чтобы установить однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предположению; если дисперсионный анализ покажет, что и математические ожидания одинаковы, то в этом смысле совокупности однородны). Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы.
Для характеристики тесноты корреляционной связи между признаками в аналитических группировках межгрупповую дисперсию сопоставляют с общей. Это отношение называется корреляционным и обозначается η2=δ2/σ2. Оно характеризует долю вариации результативного признака, вызванного действием факторного признака, положенного в основание группировки.
Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до1. Чем ближе корреляционное отношение к 1, тем большее влияние оказывает факторный признак на результативный.
Если же факторный признак не влияет на результативный, то вариация, обусловленная им, будет равна нулю (δ2=0). Корреляционное отношение также будет равно нулю (η2=0), что свидетельствует о полном отсутствии связи.
И наоборот, если результативный признак изменяется только под воздействием одного факторного признака, то вариация, обусловленная этим признаком, будет равна общей вариации (δ2= σ2), и корреляционное отношение будет равно единице (η2=1), что говорит о наличии полной связи.
Наряду с вариацией количественных признаков, может ставиться задача оценки вариации качественных признаков. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественных признаков. Так, при изучении качества изготовленной продукции её можно разделить на качественную и бракованную. В таком случае оценивается альтернативный признак. Можно считать, что эквивалентом качественного признака будет переменная, которая принимает значения 1 или 0, причём значение 1 она принимает в том случае, когда обследуемая единица обладает данным признаком, а значение 0, когда им не обладает.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►10. Определим при помощи корреляционного отношения тесноту связи между числом обслуживаемых станков и средней выработкой одного рабочего.
Таблица 11
Дневная выработка рабочего, м
Общая средняя выработка рабочего равна:
Исчислим общую дисперсию, характеризующую общую вариацию под влиянием всех факторов:
Межгрупповая дисперсия, характеризующая факторную вариацию, т.е. различия в выработке, обусловленные неодинаковым числом обслуживаемых станков, определяется по формуле:
Рассчитаем корреляционное отношение:
Общий вывод заключается в следующем. Выработка работников в основном на 93,1% определяется количеством обслуживаемых станков, и лишь 6,9% приходится на долю неучтённых факторов. Или 93,1% всей вариации объясняется тем, что часть рабочих работала на 32 станках, а часть – на 48 и только 6,9% вариации является результатом действия прочих случайных факторов, не положенных в основание группировки.◄ |
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
Дата добавления: 2014-12-23; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |
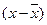
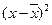
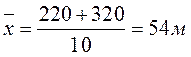 ,
,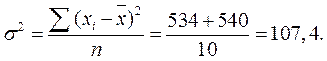

 или 93,1%.
или 93,1%.