И ДОСТОВЕРНОСТИ СВЯЗИ. МНОГОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Теперь перейдем к изучению оценки существенности корреляционного отношения с использованием уровня значимости.

Дисперсионный анализ позволяет не только определить роль случайной и систематической вариации в общей вариации, но и оценить достоверность вариации, обнаруженной методом аналитических группировок.

Определение достоверности вариации дает возможность с заданной степенью вероятности установить, вызвана ли межгрупповая вариация признаком, положенным в основание группировки, или она является результатом действия случайных причин. Для оценки существенности корреляционного отношения η² при разных условиях вероятности или значимости α.

Уровень значимости – это достаточно малое значение вероятности, отвечающее событиям, которые в данных условиях исследования будут считаться указанием на неправильность начального предположения. Чаще всего пользуются уровнями α=0,05 или α=0,01. Критические значения корреляционного отношения содержатся в специальных таблицах.

В этих таблицах распределение η² при случайных выборках зависит от числа степеней свободы факторной и случайной дисперсий. Число степеней свободы факторной дисперсии K₁=m-1, где m-число групп, а для случайной дисперсии K₂=n-m, где n-число вариант, m-число групп.

В примере №10 рабочие сгруппированы в две группы по числу обслуживаемых станков. Поэтому K₁=m-1=2-1-1, а K₂=n-m=10-2=8. По специальной таблице приложений можно найти критическое значение η², соответствующее К₁=1 и К₂=8 для уровня значимости α=0,05, которое равно: . Это значит, что только в пяти случаях из 100 может случайно возникнуть корреляционное отношение, превышающее 0,399, а в 95 случаях из 100 корреляционное отношение не может быть больше 0,399.

Затем фактическое отношение корреляционного отношения надо сравнить с критическим, табличным. Если оно окажется больше критического, то связь между результативным и факторным признаками считается существенной, если же фактическое значение η² меньше табличного, то связь между указанными признаками считается несущественной.

В рассматриваемом нами примере фактическое значение корреляционного отношения η²=0,931 больше табличного, которое составляет . Поэтому связь между числом обслуживаемых станков и выработкой является существенной.

При проверке существенности связи чаще пользуются критерием Фишера, потому что при больших числах степеней свободы его табличные значения мало изменяются в отличие от корреляционного отношения, которое требует более громоздких таблиц. Критерий Фишера представляет собой отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий, исчисленных с учетом числа степеней свободы:

(44)

Для этих отношений Р. Фишер (отсюда название «критерий Фишера») составил таблицы, по которым можно определить, какая величина F при данном числе степей свободы по факторной вариации (К₁) и остаточной вариации (К₂) дает основание утверждать с определенной вероятностью (например, 0,95; 0,99), что положенный в основание группировки признак является существенным, или не дает такого основания, и, следовательно, группировочный признак является несущественным.

В нашем примере 10 …

, .

По правилу сложения вариаций

.

Исчислим критерий Фишера F

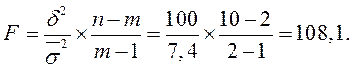
При уровне значимости α=0,05, К₁=1 и К₂=8 критическое, табличное значение F=5,32. Значит, уже при значении F=5,32 можно с вероятностью 0,95 утверждать, что группировочный признак (число обслуживаемых станков) является весьма существенным. В нашем примере он составляет F=108,1. Тем более есть основание считать, что полученные в результате группировки данные являются вполне достоверными.

Можно использовать другой способ расчёта. Зная корреляционное отношение, можно определить критерий Фишера по следующей формуле:

. (45)

Для примера 10…

Обычно используются две таблицы, позволяющие судить о предельно высокой величине показателя F при доверительных вероятностях 0,05 и 0,01 (5%-ный и 1%- уровень).

В таблице, где указана вероятность 0,05, приведены предельные теоретические значения F, которые только в 5 случаях из 100 (соответственно в другой таблице, где указана вероятность 0,01, только в одном случае из 100) могут достигать фактические значения F, если вариация всецело обусловлена только случайными причинами.

В таблице с доверительными вероятностями 0,01 соответствующие предельные теоретические значения F выше, чем в таблице с вероятностью 0,05, так как если принимается более высокая доверительная вероятность, то увеличивается и возможное предельное отношение F, обусловленное воздействием на вариацию только случайных факторов.

Табличные значения F используются как критерий для оценки фактических значений F, полученных в результате обработки статистического материала. Если F_факт>F_теор, то это значит, что очень мала вероятность того, что отношение оценочных дисперсий и, следовательно, вариация признаков обусловлена только случайными факторами. В этом случае есть основание утверждать, что между факторным группировочным признаком и результативным признаком существует взаимосвязь. Когда же F_факт<F_теор, это значит, что отношение оценочных дисперсий и вариация групповых средних факторного признака не выходят за пределы возможных случайных колебаний.

В таблице значений F в заголовках столбцов и строк указаны степени свободы вариации оценочных дисперсий. В заголовках столбцов приведены степени свободы для большей оценочной дисперсии, а в заголовках строк – для меньшей. На пересечении столбцов и строк, соответствующих степеням свободы сравниваемых оценочных дисперсий, и находится теоретическое значение F, отвечающее величине доверительной вероятности.

▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

│►11 . Предположим, что имеются 4 группы однотипных станков. Эти группы станков различаются между собой по времени производственной эксплуатации. Стоит задача выяснить, влияет ли в сложившихся условиях период эксплуатации станков на их работу.

Показателем, характеризующим работу станков, является выработка одноименных и чаще всего выпускаемых деталей на каждом станке.

Для исследования на основе случайного отбора приведены измерения выработки на пяти станках из каждой группы и получены следующие результаты:

на станках первой группы – 4, 7, 8, 10, 6 деталей в час;

второй группы – 9, 10, 10, 5, 6 деталей в час;

третьей группы – 9, 11, 8, 7, 10 деталей в час;

четвертой группы – 10, 5, 4, 6, 5 деталей в час.

Составим расчетную табл. 12.

Таблица 12

Расчетная таблица

Группа станков	Выработка деталей в час х	Суммы вариантов	Групповые средние и общая средняя	Отклонения групповых средних от средней общей	Квадраты отклонений	Отклонения вариантов от групповых средних	Квадраты отклонений
Первая				-0,5	0,25	-3 -1
Вторая				+0,5	0,25	-3 -2
Третья				+1,5	2,25	-1 -2
Четвертая				-1,5	2,25	-1 -2 -1
Суммы, средняя и девиация	n=20	=150	=7,5	-	D22=5	-	D21=74

Следовательно, внутригрупповая девиация D²₁=74, межгрупповая девиация D²₂=5, а общая девиация D²= D²₁+ D²₂=74+5=79. Число степеней свободы для общей девиации n-1=20-1=19, для внутригрупповой девиации n-m=20-4=16, а для межгрупповой девиации m-1=4-1=3. Определим оценочные дисперсии:

Вследствие того, что девиация делится на различное число степеней свободы, то

Находим значение критерия F:

В соответствии с числом степеней свободы для S²₁, равным 16, и для S²₂, равным 3, в таблице для 5%-ного уровня распределения F на пересечении соответствующего столбца и строки находим значение этого показателя F_факт=8,69, а для 1%-ного уровня распределения F_теор=26,83.

Так как даже для доверительной вероятности 0,05 (5%-ный уровень) F_факт<F_теор, следует считать, что длительность эксплуатации станков в сложившихся условиях не влияет на работу станков, на их производительность. Нулевая гипотеза, т.е. то, что межгрупповая вариация производительности станков всецело обусловлена случайными факторами, остается не опровергнутой [8].

.

Об отсутствии связи между длительностью работы станков и их производительностью свидетельствует низкое значение корреляционного отношения. ◄

▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲

Следует отметить, что принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие.

Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценки межфакторного взаимодействия.

Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анализа (в варианте ее компьютерного использования), несомненно, более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие.

Необходима оценка достоверности влияния не только каждого положенного в основание группировки фактора в отдельности, но и результата их взаимодействия.

Последний определяется как разность между эффектом совместного влияния двух группировочных признаков и суммой эффектов влияния каждого из этих факторных признаков, взятых в отдельности. Это осложняет расчеты суммы квадратов отклонений и числа степеней свободы вариации. Но сам принцип дисперсионного анализа, заключающийся в сопоставлении факторной дисперсии со случайной для оценки достоверности результатов статистической группировки, неизменен при любом числе признаков группировки.

В основе применения дисперсионного анализа лежит закон разложения дисперсий признака на составляющие. Общая вариация (D₀) результативного признака при группировке может быть разложена на следующие составные части: на межгрупповую (D_м), связанную с группировочными признаками; и на остаточную (внутригрупповую D_в), не связанную с группировочным признаком.

Для проведения дисперсионного анализа необходимо установить источники варьирования признака, объем вариации по источникам; определить число степеней свободы для каждой компоненты вариации и дисперсии для каждой составляющей (межгрупповой и внутригрупповой).

РЕЗЮМЕ

Аналитические группировки и другие приёмы исследования при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного и корреляционного анализов.

Дисперсионный анализ позволяет оценить достоверность вариации, обнаруженной методом аналитических группировок и доказать существенность связей между признаками. В основе применения дисперсионного анализа лежит закон разложения дисперсий признака на составляющие.

Связь между общей, межгрупповой и внутригрупповой дисперсиями получила в статистке название закона сложения (разложения) вариации. Для проведения дисперсионного анализа необходимо установить источники варьирования признака, объем вариации по источникам; определить число степеней свободы для каждой компоненты вариации и дисперсии для каждой составляющей (межгрупповой и внутригрупповой).

Значимость определяют с помощью критерия Фишера, представляющего собой отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий, исчисленных с учетом числа степеней свободы. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие.

.

В этой главе приведено:

▼   ▲

v Общие понятия и цели дисперсионного анализа.

v Оценка существенности корреляционного отношения с использованием уровня значимости.

v Проверка существенности связи с применением критерия Фишера.

v Многофакторный дисперсионный анализ.