КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определим возможности применения коэффициента конкордации
Для оценки степени тесноты связи между несколькими порядковыми признаками применяется коэффициент конкордации. С помощью коэффициента конкордации обычно измеряют согласованность мнений экспертов.
При отсутствии связанных рангов коэффициент конкордации рассчитывается по формуле
(31)
где m – число факторов; n – число ранжируемых единиц; S – сумма квадратов отклонений сумм рангов наблюдений (объектов) от их общего среднего ранга:
(32)
где 
- ранг i-го фактора у j-й единицы, i=1,….,m; j=1,….,n.
Коэффициент конкордации w принимает значение в пределах от 0 до 1, w=1 означает полную согласованность ранжировок, при w=0 – полную несогласованность.
При наличии связанных рангов формула коэффициента конкордации преобразуется:
. (33)
Для проверки значимости (отличия от нуля) коэффициента конкордации используют критерий 
.
Расчетное значение критерия находят по формуле
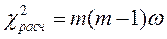. (34)
Табличное значение 
находят по таблице распределения 
с заданной вероятностью и числом степеней свободы, равным n-1.
Если 
, то гипотеза об отсутствии связи отклоняется на уровне значимости α.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►8. Экспертам было предложено оценить влияние группы факторов при выборе варианта инновационного проекта (табл. 8)., выставив соответствующие оценки.
Таблица 8
Сумма квадратов отклонений рангов равна:
Коэффициент конкордации:
Полученное значение свидетельствует о высокой согласованности мнений экспертов. Для проверки статистической значимости полученного коэффициента конкордации воспользуемся критерием «хи-квадрат». Расчетное значение критерия составит:
Примем доверительную вероятность, равную 95%. Число степеней свободы равно n-1=5-1=4. Табличное значение критерия «хи-квадрат» равно 9,5. Так как расчетное значение больше табличного, то с вероятностью 95% можно утверждать, что полученный коэффициент конкордации значим и, следовательно, мнения экспертов по выбору конкретного инновационного проекта согласованы. ◄
|
.
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Дата добавления: 2014-12-23; просмотров: 265; Мы поможем в написании вашей работы!; Нарушение авторских прав |