
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рассмотрим применение коэффициента корреляции рангов Спирмэна
Формула коэффициента корреляции рангов Спирмэна получена из формулы коэффициента парной корреляции:
 , (19)
, (19)
где  - ранг i-й единицы совокупности по переменной х;
- ранг i-й единицы совокупности по переменной х;  - средний ранг по переменной х;
- средний ранг по переменной х; 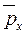 - ранг i-й единицы совокупности по переменной у,
- ранг i-й единицы совокупности по переменной у,  средний ранг по переменной у.
средний ранг по переменной у.
Очевидно, что коэффициент ранговой корреляции изменяется, так же, как и коэффициент парной корреляции, в интервале от -1 до +1.
При отсутствии связанных рангов путем преобразований приведенной формулы Спирмэном была получена формула коэффициента ранговой корреляции, который обычно обозначается греческой буквой p:
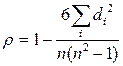 , (20)
, (20)
где di – разность рангов по переменным х и у для i-й единицы совокупности; n- число наблюдений.
Ранговый коэффициент корреляции изменяется, так же как и коэффициент парной корреляции, в интервале от -1 до +1 и оценивает силу линейной зависимости между рангами.
При наличии связанных рангов необходимо пользоваться скорректированной формулой коэффициента корреляции рангов Спирмэна. Пусть определяется теснота связи между к-м и l-м признаками, в рядах значений которых имеется соответственно q и g групп объединенных рангов. Тогда формула коэффициента корреляции рангов Спирмэна примет вид
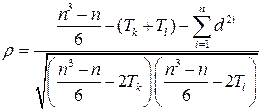 , (21)
, (21)
где
 , (22)
, (22)
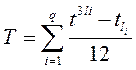 , (23)
, (23)
где t и tli – число единиц в i-й группе объединенных рангов соответствующего признака.
Статистическая значимость коэффициентов корреляции Спирмэна проверяется с помощью специальных таблиц.
Если абсолютная величина расчетного значения рангового коэффициента корреляции больше табличного, нулевая гипотеза отвергается и корреляция признается статистически значимой.
Дата добавления: 2014-12-23; просмотров: 285; Мы поможем в написании вашей работы!; Нарушение авторских прав |