СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗУЧЕНИЯ КОРРЕЛЯЦИОННОЙ СВЯЗИ

Определяющая роль в выборе формы связи между явлениями принадлежит теоретическому анализу. Так, например, выпуск продукции и стоимость основных фондов, урожайность и количество внесенных удобрений взаимосвязаны между собой.

Анализ показывает, что чем больше имеет предприятие основных фондов (факторный признак); тем больше при прочих равных условиях оно выпускает продукции (результативный признак). С ростом факторного признака здесь, как правило, равномерно растет и результативный, поэтому зависимость между, ними может быть выражена уравнением прямой

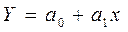, (1)

которое носит название линейного уравнения регрессии.

Однако с помощью теоретического анализа не всегда удается установить форму связи. В таких случаях приходится только предполагать о наличии определённой формы связи.

Проверить эти предположения можно при помощи графического анализа, который используется для выбора формы связи между явлениями, хотя графический метод изучения связи применяется и самостоятельно.

Если на оси абсцисс откладывать значения факторного признака X, на оси ординат — значения результативного признака у, а на график нанести точки, соответствующие значениям х и у, то получим корреляционное поле.

На практике изучение взаимосвязи между признаками часто базируется на значительном числе наблюдений, материалы которых группируются по двум взаимосвязанным признакам (х и у).

По характеру расположения точек на поле можно сделать вывод о направлении и силе связи. Чем теснее точки группируются вокруг линии характеризующей форму связи, тем сильнее связь между факторным и результативным признаками.

Если же точки расположены беспорядочно на графике, то связь между признаками отсутствует, как это показано на рис. 2.

Рис.2. Распределение корреляционного поля при различных видах связи: а - прямая связь; б - обратная

Корреляционный анализ применяется для определения тесноты корреляционной связи между переменными х и у. Теснота корреляционной связи может быть измерена эмпирическим корреляционным отношением , когда (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: .

Говоря о корреляционном отношении как о показатели измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения - теоретическое.

Теоретическое корреляционное отношение представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выравненных значений результативного признака , т.е. рассчитанных по уравнению регрессии, со средним квадратическим отношением эмпирических (фактических) значений результативности признака :

, (2)

где ,

, (3)

тогда , (4)

Изменение значения объясняется влиянием факторного признака.

В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е. , где - отражает вариацию у за счет всех остальных факторов, кроме х, т.е. является остаточной дисперсией:

, (5)

Тогда формула теоретического корреляционного отношения примет вид

(6)

или , (7)

Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности).

Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора [10]