ИЗМЕРЕНИЕ ТЕСНОТЫ КОРРЕЛЯЦИОННОЙ СВЯЗИ

Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком.

При криволинейных связях теоретическое корреляционное отношение часто называют индексом корреляции R. При значительной корреляции расчет по этим формулам значительно проще, так как отклонение , как правило, по значению меньше, чем отклонение .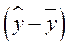

Как видно из формул, корреляционное отношение может находиться в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.

Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - линейный коэффициент корреляции:

, (8)

где n-число наблюдений.

Для практических вычислений при малом числе наблюдений линейный коэффициент корреляции удобнее исчислять по следующей формуле:

(9)

Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значение в интервале:

Отрицательные значения указывают на обратную связь, а положительные на прямую. При =0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при = 1 связь - функциональная.

Квадрат линейного коэффициента корреляции 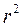называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его значение всегда заключено в пределах от 0 до 1.

Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

Факт совпадений и несовпадений значений теоретического корреляционного отношения и линейного коэффициента корреляции используются для оценки формы связи.

Посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции – только прямолинейной. Следовательно, значения и совпадают только при наличии прямолинейной связи. Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов и 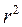не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.

Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

При линейной однофакторной связи t-критерий можно рассчитать по формуле

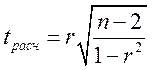, (10)

где (n-2) – число степеней свободы при заданном уровне значимости α и объеме выборки n.

Если полученное значение превосходит табличное значение критерия , то практически невероятно, что найденное значение обусловлено только случайными колебаниями [6].

2.4. МНОГОФАКТОРНЫЙ КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, т.е. эти явления многофакторны. Между факторами существуют сложные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель факторов при фиксированном положении остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя. [6]