
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КОРРЕЛЯЦИЯ КАТЕГОРИЗИРОВАННЫХ (НОМИНАЛЬНЫХ) ПЕРЕМЕННЫХ
Основой изучения связи номинальных переменных служит таблица сопряженности – двухмерное распределение единиц совокупности по переменным х и у (табл. 9).
Таблица 9
| Переменная х | Переменная у | Итого | ||||
| y1 | y2 | y3 | … | yр | ||
| x1 | n11 | n12 | n13 | … | n1p | n1. |
| x2 | x21 | x22 | x23 | … | x2p | n2. |
| x31 | x32 | x33 | … | x3p | n3. | |
| … | … | … | … | … | … | … |
| хm | xm1 | xm2 | xm3 | … | xmp | nm. |
| Итого | n.1 | n..2 | n..3 | … | n.p | n |
В итоговых частотах точкой обозначено суммирование по одному из подстрочных значков.
Частоты, стоящие в клетках таблицы, называются клеточными частотами. Именно по их значениям судят о наличии и тесноте связи. Если единицы совокупности концентрируются в диагональных клетках таблицы, то налицо наличие связи; если же такой концентрации не наблюдается – связи может не быть.
Факт наличия связи устанавливается с помощью критерия  :
:
 , (35)
, (35)
где nij – фактическая клеточная частота, т.е. число единиц с i-м значением признака х и j-м значением признака у; - теоретическая клеточная частота, отвечающая предположению о независимости переменных х и у, т.е. отсутствию связи.
Как известно, вероятность двух независимых событий равна произведению их вероятностей:
 . (36)
. (36)
Для того чтобы от вероятностей (частностей) перейти к частотам, вероятность нужно умножить на n. Получаем формулу клеточной частоты
 , (37)
, (37)
т.е. итог по i-й строке нужно умножит на итог по j-му столбцу, и разделить на общее число данных.
Сумма теоретических частот во всех клетках таблицы равна общему числу наблюдений n:

Сумма теоретических частот по строкам и столбцам таблицы равна соответственно ni и nj:


Таким образом, теоретические частоты – это перераспределение исходных данных в предположении, что связь между переменными х и у отсутствует.
Величина  показывает, насколько велико расхождение фактических частот с теми, которые были бы, если бы х и у были независимыми. Такое расхождение так или иначе всегда будет, поэтому существует таблица критических значений критерия
показывает, насколько велико расхождение фактических частот с теми, которые были бы, если бы х и у были независимыми. Такое расхождение так или иначе всегда будет, поэтому существует таблица критических значений критерия  , которая содержит предельно возможные значения статистики
, которая содержит предельно возможные значения статистики  в случае предположения о независимости переменных.
в случае предположения о независимости переменных.
Распределение  зависит от числа степеней свободы и уровня значимости α. Число степеней свободы определяется следующим образом:
зависит от числа степеней свободы и уровня значимости α. Число степеней свободы определяется следующим образом:
 , (38)
, (38)
где m – число категорий переменной х, или число строк таблицы сопряженности; p – число категорий переменной у, или число столбцов таблицы сопряженности; mp – число клеток таблицы сопряженности. Уровень значимости обычно принимается равным α – 0,05 или 0,01 (5% или 1%).
Вычисленное по вышеуказанной формуле значение  сравнивается с критическим (табличным) значением
сравнивается с критическим (табличным) значением  при данном числе степеней свободы и принятом уровне значимости. Если
при данном числе степеней свободы и принятом уровне значимости. Если  , то делается вывод о наличии связи признаков х и у, и наоборот, если
, то делается вывод о наличии связи признаков х и у, и наоборот, если  , то гипотеза о независимости х и у не отклоняется, т.е. наличие связи может считаться доказанным.
, то гипотеза о независимости х и у не отклоняется, т.е. наличие связи может считаться доказанным.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
 |
│►9. При анализе работы фирмы, оказывающей сантехнические услуги как коммерческим организациям, так и индивидуальным заказчикам, возникла необходимость оценить связь между типами клиентов и качеством обслуживания. С этой целью была построена таблица сопряженности (табл. 10):
Таблица 10
Соотношение типа клиента и качества обслуживания
| Клиенты | Качество обслуживания | Количество обслуженных | |||
| устраивает | не устраивает | ||||
| Компании | 34,8 | ||||
| Индивидуальные заказчики | 368,8 | 96,2 | |||
| Итого |
 Анализируя данные табл. 10, видим, что среди обслуженных компаний лишь 10% высказали претензии к качеству обслуживания, тогда как из индивидуальных заказчиков доля тех, кого не устроило качество работ, составила 24%. Чтобы удостовериться, что связь между типом клиента и качеством обслуживания существует, вычислим значения. Для этого рассчитаем теоретические частоты, которые запишем в клетках таблицы в правом верхнем углу.
Анализируя данные табл. 10, видим, что среди обслуженных компаний лишь 10% высказали претензии к качеству обслуживания, тогда как из индивидуальных заказчиков доля тех, кого не устроило качество работ, составила 24%. Чтобы удостовериться, что связь между типом клиента и качеством обслуживания существует, вычислим значения. Для этого рассчитаем теоретические частоты, которые запишем в клетках таблицы в правом верхнем углу.
 ;
;  ;
;
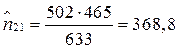 ;
;  .
.
Учитывая, что мы имеем дело с таблицей  (четырехклеточной), можно было бы не вычислять
(четырехклеточной), можно было бы не вычислять  и
и  , а получена их разность
, а получена их разность  и
и  .
.
Поскольку теоретические клеточные частоты – рассчитанные величины, они могут быть нецелыми числами, как получилось в нашем примере. Сумма всех теоретических частот равна объему выборки, n=633. Итоги по строкам и столбцам таблицы равны маргинальным частотам: (133,2+34,8=168), (133,2+368,8=502).
Вычислим значение  :
:
 .
.
Табличное значение  при числе степеней свободы
при числе степеней свободы  и уровне значимости α=0,05 (т.е. при 95% доверительной вероятности) составляет 3,84.
и уровне значимости α=0,05 (т.е. при 95% доверительной вероятности) составляет 3,84.
А величина 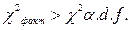 . Следовательно, наличие связи может считаться доказанным и действительно, от типа клиента зависит качество обслуживания. ◄
. Следовательно, наличие связи может считаться доказанным и действительно, от типа клиента зависит качество обслуживания. ◄
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
После того как связь установлена, приступают к ее измерению, поскольку  не является мерой связи. Величина этого критерия зависит от объема совокупности, числа строк и столбцов таблицы,
не является мерой связи. Величина этого критерия зависит от объема совокупности, числа строк и столбцов таблицы,  , т.е. значение
, т.е. значение  может быть сколь угодно большим.
может быть сколь угодно большим.
Меры связи, используемые в статистике, изменяются в интервале от 0 до1. И это очень удобно с точки зрения интерпретации: выделение слабых связей, умеренно тесных или сильных.
Дата добавления: 2014-12-23; просмотров: 404; Мы поможем в написании вашей работы!; Нарушение авторских прав |