
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПОСТРОЕНИЕ И СТАТИСТИЧЕСКИЙ АНАЛИЗ ДВУХФАКТОРНОЙ ЛИНЕЙНОЙ МОДЕЛИ (ТРЕХМЕРНОЙ РЕГРЕССИИ)
Для расчета параметров простейшего уравнения множественной линейной двухфакторной регрессии
 , (58)
, (58)
где  - расчетные значения зависимой переменной (результативного признака); х1, х2 – независимые переменные (факторные признаки); а0, а1, а2 – параметры уравнения.
- расчетные значения зависимой переменной (результативного признака); х1, х2 – независимые переменные (факторные признаки); а0, а1, а2 – параметры уравнения.
Построим следующую систему нормальных уравнений
 (59)
(59)
Параметры этой системы могут быть найдены, например, методом К. Гаусса.
Построение и анализ трехмерной регрессионной модели рассмотрим на конкретном примере.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►14. По выборочным данным, представленным в табл. 8 , о выборке деталей за смену 20 рабочими цеха требуется выявить зависимость производительности труда у от двух факторов: внутрисменных простоев х1 и квалификации рабочих х2.
Таблица 15
Стохастическая связь между производительностью труда, внутрисменными простоями и квалификацией рабочих
Теоретический анализ исходных данных позволяет установить наличие причинно-следственной связи факторных признаков (внутрисменных простоев и квалификации рабочих) с результативным показателем – производительностью труда. Регрессионную двухфакторную модель построим в линейной форме
и проверим ее адекватность.
Для нахождения параметров этого уравнения произведем вычисления вспомогательных величин, которые запишем в табл. 16.
Таблица 16 Расчет параметров и оценка линейной двухфакторной регрессионной модели
Составим систему нормальных уравнений:
Решая данную систему методом К. Гаусса, получаем а0=81,03; а1=-0,41; а2=3,37. Уравнение множественной регрессии, выражающее зависимость производительности труда
Вычислим по этому уравнению |
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Дата добавления: 2014-12-23; просмотров: 440; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 =11
=11
 =4
=4
 =90
=90
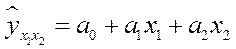




 ;
;  ;
;  ;
;  ;
;  ;
; 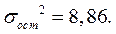
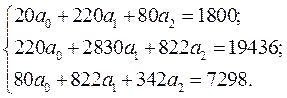
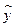 от внутренних простоев х1 и квалификации рабочих х2, примет вид:
от внутренних простоев х1 и квалификации рабочих х2, примет вид: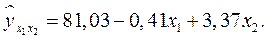
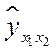 и занесем полученные значения в табл. 16. ◄
и занесем полученные значения в табл. 16. ◄