
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проведём обзор выбора вида моделей с оценкой их параметров
Для отображения зависимости переменных могут использоваться показательная, параболическая и многие другие функции. Однако в практической работе наибольшее распространение получили модели линейной взаимосвязи, т.е. когда факторы входят в модель линейно.
Линейная модель множественной регрессии имеет вид
Yi = а0 + а1хi1 + а2хi2 + ... + атхim + 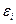 . (1)
. (1)
Анализ уравнения (1) и методика определения его параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи этого уравнения
Y= Хa +  ,
,
где Y - вектор зависимой переменной размерности (n х 1), представляющий собой n наблюдений значений уi;
Х- матрица независимых переменных, элементы которой суть n x т наблюдения значений т независимых переменных Х1, X2,...,Xm, размерность матрицы Х равна (n х т);
a - подлежащий оцениванию вектор неизвестных параметров размерности (m x l);
 - вектор случайных отклонений (возмущений) размерности (n x 1).
- вектор случайных отклонений (возмущений) размерности (n x 1).
Учитывая преобразования, можно записать:
Y= 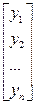 , Y=
, Y= 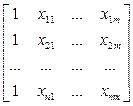 , a=
, a= 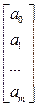 .
.
Уравнение (1) содержит значения неизвестных параметров уравнения регрессии а0, а1, а2,..,ат. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки.
Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:
Y = X∙a +  =
= 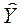 + e, (2)
+ e, (2)
где a - вектор оценок параметров;
е - вектор «оцененных» отклонений регрессии,
е = Y - Х∙a - остатки регрессии;
 - оценка значений Y, равная Х∙а.
- оценка значений Y, равная Х∙а.
Для оценивания неизвестного вектора параметров a используется МНК. Формула для вычисления параметров регрессионного уравнения имеет вид
а = (ХT Х)-1 ХТ Y. (3)
В случае зависимости переменной Y от одного фактора X имеем
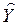 = а0+a1Х.
= а0+a1Х.
Используя соотношение (3), получаем значения параметров уравнения регрессии:
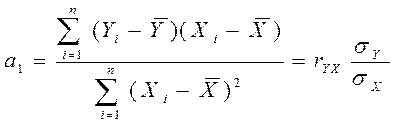 ,
,
а0= 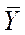 +a1
+a1 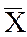 .
.
Дата добавления: 2014-12-23; просмотров: 347; Мы поможем в написании вашей работы!; Нарушение авторских прав |