Рассмотрим практическую оценку влияния отдельных факторов на зависимую переменную в построенной модели регрессии.

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако с их помощью непосредственно нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости.

Для устранения таких различий и противоречий для анализа и интерпретации применяются средние частные коэффициенты эластичности Э(j)и b-коэффициенты b(j), которые рассчитываются соответственно по формулам:

,

,

где 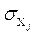- среднее квадратическое отклонение фактора j.

Коэффициент эластичности 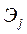показывает, на сколько процентов изменяется зависимая переменная при изменении j-го фактора на 1 %. Однако здесь не учитывается степень колеблемости факторов.

Бета-коэффициент характеризует часть величины средне­го квадратического отклонения а _х на которую изменится зависимая переменная Y с изменением соответствующей независимой переменной Х_j на величину своего среднего квадратического отклонения при фиксиро­ванном постоянном уровне значений остальных независимых пере­менных.

Указанные коэффициенты позволяют ранжировать факторы по степени их влияния на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов на результативный признак можно оценить по величине дельта-коэффициентов Dj

Dj=r_Yj b_j/R²,

где r_Yj - коэффициент парной корреляции между j-ым фактором (j = 1, ..., т) и зависимой переменной.