
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Пример 3.При анализе влияния на цену товара ряда факторов был включен, кроме объема партии, еще один признак - расходы на рекламу за предыдущий месяц (тыс. руб.). Поставлена задача проведения многофакторного анализа связи результативного признака у и двух факторных х1 и х2.
Данные для расчета коэффициентов корреляции rx1x2 приведены в табл. 14.
Таблица 14
Расчетная таблица
| Фирмы | Расходы на рекламу товара за прошлый месяц, тыс. руб., х2 | х2у | х2х1 | х22 |
| Итого |
Линейный коэффициент корреляции применяется для определения тесноты прямолинейной связи между факторным и результативным признаками и исчисляется по формуле:
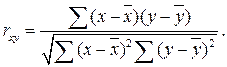
Следует помнить, что при оценке существенности коэффициента корреляции пользуются специальной таблицей критических значений 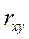 .
.
Для определения тесноты криволинейной связи применяют индекс корреляции, который определяется по формуле:
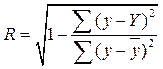 ,
,
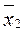 =9 тыс. руб.;
=9 тыс. руб.; 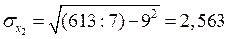 тыс. руб.
тыс. руб.
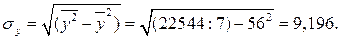
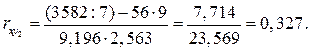
Корреляция между переменными х1 и х2

Рассмотрим матрицу коэффициентов парной корреляции, приведенную в табл. 15.
Таблица 15
Матрица коэффициентов парной корреляции
| Признаки | у | х1 | х2 |
| у | -0,865 | 0,327 | |
| х1 | -0,276 | ||
| х2 |
Сравнение коэффициентов парной корреляции показывает, что связь обеих объясняющих переменных, как х1, так и х2, с результативной переменной у более тесная, чем между собой. Следовательно, объем партии и расходы на рекламу могут быть совместно включены при проведении анализа факторов, влияющих на уровень цены товара.
Вычислим коэффициенты частной корреляции 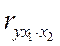 и
и 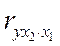 :
:
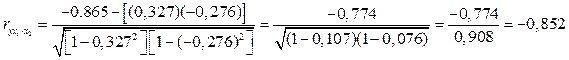 ,
,
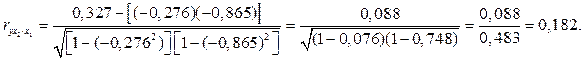
Сопоставляя полученные значения коэффициентов частной корреляции с коэффициентами парной корреляции, видим, что коэффициенты частной корреляции меньше парных коэффициентов по абсолютной величине.
Измерим тесноту связи у с х1 и х2 совместно, т.е. вычислим коэффициент множественной корреляции. Сначала определим коэффициент множественной детерминации. В случае трех переменных для этой цели можно воспользоваться формулой
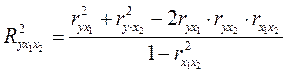 ,
,
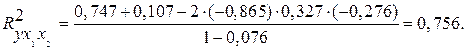
Тогда значение коэффициента множественной корреляции составит 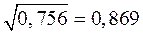 .
.
Можно заключить, что факторные признаки влияют на 75,6% от всего объёма влияния всех возможных факторов на цену товара. Остальное влияние (24,4%) определяется неучтенными переменными.
Пример 4.Установим зависимость между факторным признаком в виде себестоимости 1т цемента и производственными мощностями десяти обследуемых заводов составим. Для вычислений составим вспомогательную расчетную табл. 16, в которой приведена также исходная информация для анализа.
Таблица 16
Зависимость между размерами производственных
мощностей и себестоимостью продукции ряда предприятий
| № завода | Производит. заводов в месяц (х, тыс.т.) | Себе-сть 1т.(у), руб. | 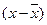
| 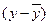
| 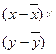
| 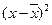
| 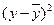
|
| 7,0 | -3,6 | -165,6 | 12,96 | ||||
| 7,6 | -3,0 | -126,0 | 9,00 | ||||
| 8,0 | -2,6 | -67,6 | 6,76 | ||||
| 9,0 | -1,6 | -9,6 | 2,56 | ||||
| 10,0 | -4 | -0,6 | +2,4 | 0,36 | |||
| 10,8 | -14 | +0,2 | -2,8 | 0,04 | |||
| 12,0 | -24 | +1,4 | -33,6 | 1,96 | |||
| 14,0 | -34 | +3,4 | -115,6 | 11,56 | |||
| 17,0 | -44 | +6,4 | -281,6 | 40,96 | |||
| Итого | 95,4 | -800 | 86,16 | ||||
| В среднем | 10,6 |
Определим линейный коэффициент корреляции
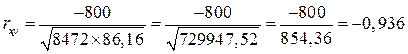 .
.
Значение линейного коэффициента корреляции равного 0,936 показывает, что между производительностью заводов и себестоимостью одной тонны цемента существует весьма тесная обратная связь, т.е. с увеличением производственной мощности заводов себестоимость 1т цемента снижается.
В нашем примере 9 пар возможных вариант. Для простой корреляции n на 2 меньше, чем число пар вариант. Значит, n = 9-2 =7. Рассчитанный нами коэффициент корреляции равен -0,936, т.е. он больше своего табличного значения (0,6664 и 0,7977) при уровне вероятности 0,95 и 0,99.
Следовательно, исчисленный нами коэффициент корреляции существенен и достаточно точно отражает тесноту связи между производственной мощностью заводов и себестоимостью 1т цемента.
Пример 5.Проведём оценку вариации приведенных признаков для установления наличия связи между ними. Рассчитаем по данным табл.17 дисперсии групповых средних нераспределенной прибыли и инвестиций в основные фонды, млн руб.
Таблица 17
Исходные и расчетные данные
| № предприятия | Инвестиции в основные фонды, млн.руб., х | 
|
| 0,06 | 0,0036 | |
| 0,04 | 0,0016 | |
| 0,44 | 0,1936 | |
| 0,6 | 0,36 | |
| 0,90 | 0,81 | |
| 0,12 | 0,0144 | |
| 0,20 | 0,04 | |
| 0,36 | 0,1296 | |
| 0,80 | 0,64 | |
| 0,60 | 0,36 | |
| 0,18 | 0,0324 | |
| 0,40 | 0,16 | |
| 0,53 | 0,2809 | |
| 0,65 | 0,4225 | |
| 0,42 | 0,1764 | |
| 0,70 | 0,49 | |
| 0,50 | 0,25 | |
| 0,35 | 0,1225 | |
| 0,20 | 0,04 | |
| 0,70 | 0,49 | |
| 0,40 | 0,16 | |
| 0,73 | 0,5329 | |
| 0,62 | 0,3844 | |
| 0,70 | 0,49 | |
| 0,30 | 0,09 | |
| Итого: | 11,5 | 6,68 |
Определим среднее значение факторного признака
xср = ∑(x·f)/∑f=11, 57/25=0,46.
Таблица 18
| № группы | Группы предприятий по нераспределенной прибыли, млн.руб. | Число предприятий f | Инвестиции в среднем на одно предприятие, млн. руб, Х | x- xср | (x-xср)2 | (x-xср)2f |
| А | Б | |||||
| I | 2,0-2,8 | 0,10 | -0,36 | 0,13 | 0,52 | |
| II | 2,8-3,6 | 0,23 | -0,23 | 0,05 | 0,15 | |
| III | 3,6-4,4 | 0,40 | -0,06 | 0,0036 | 0,02 | |
| IV | 4,4-5,2 | 0,62 | 0,16 | 0,0256 | 0,21 | |
| V | 5,2-6,0 | 0,78 | 0,32 | 0,1024 | 0,41 | |
| Итого | 2,13 | --- | --- | 1,31 |
Определим среднее значение факторного признака
xср = ∑(x*f)/∑f=11, 57/25=0,46.
Используя полученные значения и результаты промежуточных вычислений в табл.18, найдем межгрупповую дисперсию
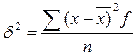 ,
,
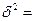 1,31/25=0,05.
1,31/25=0,05.
Для расчета общей дисперсии будем использовать табл. 18.
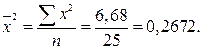
Общая дисперсия равна:
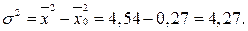
Коэффициент детерминации найдем по формуле:
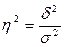 , следовательно,
, следовательно,  .
.
Это значит, что только 1,2% выпуска продукции по предприятиям зависят от изменения вложений (инвестиций) в основные фонды.
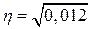 = 0,11.
= 0,11.
Связь между нераспределенной прибылью и инвестициями в основные фонды очень слабая.
Дата добавления: 2014-12-23; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |