ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ

Пример 1. По данным табл.11 вычислим параметры уравнения линейной парной регрессии, описывающего зависимость цены товара (у) от объема продаж (объема партии) (х).

Таблица 11

Цены и объём реализации товаров

Для составления уравнения регрессии в виде линейной связи 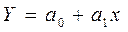,необходимо определить параметры а₀ и а₁. Они исчисляются обычно с использованием МНК путем решения системы двух нормальных уравнений:

;

.

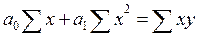Проведём вычисления табличным способом (табл.12), что сделает вычисления более наглядными.

Таблица 12

Расчетная таблица

Номер фирмы	хi	уi	хi уi	хi2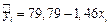
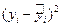
					65,18	4,82	23,2149
					54,96	0,04	0,0019
					57,88	7,12	50,7215
					43,27	1,73	2,9906
					52,03	-2,03	4,1417
					50,57	-5,57	31,0737
					68,10	-6,10	37,2503
						Х	149,3946

;

.

Значение параметра а также можно получить и на основе соотношения между и :

.

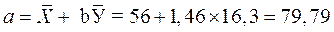Получаем уравнение парной регрессии для описания зависимости цены и объема партии товара:

.

Параметр а в данном примере выполняет роль доводки до соотношения между средними и .

Можно предположить, что а – эта та часть цены, которая не зависит от объема партии. Параметр b (коэффициент регрессии) показывает, что с ростом объема партии на одну тысячу штук цена падает на 1 руб. 46 коп.

Коэффициент регрессии можно найти на основе коэффициента корреляции, используя зависимости:

,

, или

По данным нашего примера получим

руб./шт.; 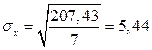тыс. шт.

Получаем: руб./шт

Пример 2. По данным, приведенным в табл. 13, вычислим по уравнению регрессии 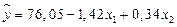ожидаемые значения цены товара.

Таблица 13

Анализ цены товара

Фирмы	уi (руб.)
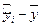
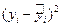
		64,91	8,91	5,09	25,9081
		56,33	0,33	-1,33	1,7689
		57,81	1,81	7,19	51,6961
		43,95	-12,05	1,05	1,1025
		50,77	-5,23	-0,77	0,5929
		49,69	-6,31	-4,69	21,9961
		68,43	12,43	-6,43	41,3449
Итого			Х	Х	144,4095

Из табл. 13 видно, что у фирм 4, 5 и 6 ожидаемая цена (если бы установленные закономерности влияния объясняющих переменных действовали без отклонений) была бы ниже средней по совокупности. Причину этого можно найти, сравнивая конкретные значения переменных х₁ и х₂ со средними значениями. Скажем, для фирмы 4 имеем:

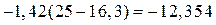руб. – для переменной х₁;

руб. – для переменной х₂,

т.е. в большей степени отклонение от средней цены вызвано большим объемом партии товара.

Второе отклонение - остаточная часть вариации у, не объясненная регрессией. В то же время при высоком значении R² эту разность можно интерпретировать как результат отличия силы влияния объясняющих переменных в условиях конкретной фирмы от средней силы влияния, т.е.

,

.

Разность возникает за счет использования воздействия факторных переменных на результативную переменную, т.е. за счет .

Так, у фирмы 2 влияние факторных признаков (объема партии) и затрат на рекламу недоиспользуется, тогда как фирма 3 добивается полной отдачи от этих факторов.

Регрессия используется для прогнозирования. По уравнению регрессии можно рассчитать ожидаемую цену, например, при объеме партии товара 20 тыс. шт. и затратах на рекламу 1 тыс. руб.:

Это точечный прогноз. Он оправдан, если используемые значения объясняющих переменных находятся внутри интервала фактических значений факторов. Если же они выходят за эти границы, то правильнее дать интервальную оценку ожидаемого значения результата.

Предполагая, что объем партии товара составит 30 тыс. шт., а затраты на рекламу – 4 тыс. руб. (что выходит за рамки интервалов фактических значений факторов), ожидаемая цена по точечному прогнозу составит:

руб.,

определим интервальную оценку.

Средняя ошибка прогноза для индивидуального значения образуется из ошибки прогноза положения линии регрессии и остаточной вариации переменной у:

,

руб.

В знаменателе подкоренного выражения указано число степеней свободы остаточной дисперсии: df=n-m, где m – число параметров в уравнении регрессии; n – число наблюдений.

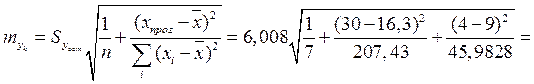
отсюда

руб.

Согласно интервальному прогнозу цена товара с вероятностью 0,95 будет находиться в пределах: 34,81 руб. 1,96 9,51 руб., т.е. от 16 руб. 21 коп. до 53 руб. 41 коп.

Очевидно, что ценность такого прогноза незначительна, интервальная оценка цены дала значения цены в слишком широких границах.