Рассмотрим порядок проведения проверки качества построенной модели

Качество модели оценивается для математических моделей стандартным образом: по адекватности и точности на основе анализа остатков регрессии «е».

Расчетные значения указанных параметров получаются путем подстановки в модель фактических значений всех включенных факторов.

Анализ остатков.Анализ остатков позволяет получить представление о том, насколько хорошо подобрана сама модель и как правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности почти независимые), одинаково распределенные случайные величины. При этом в классических методах регрессионного анализа предполагается нормальный закон распределения остатков.

Исследование остатков полезно начинать с изучения их графического представления. Нередко встречаются ситуации, когда остатки содержат тенденцию или подвержены циклическим колебаниям. В этом случае говорят о наличии автокорреляции остатков. Иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения результативного признака. В других случаях автокорреляция указывает на наличие какой-то достаточно сильной зависимости, неучтенной в модели. Так, при подборе простой линейной зависимости между Y и X график остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной) или включения в модель периодических компонент.

Наиболее распространены два метода определения автокорреляции остатков. Первый метод- это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод- использование критерия Дарвина - Уотсона(прил. 3) и расчет величины

.

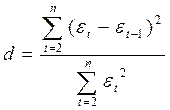Здесь d есть отношение суммы квадратов разностей по­следовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Коэффициент автокорреляции остатков определятся из зависимости

,

где , .

Можно показать, что есть соотношение

d » 2*(1- ).

Если в остатках существует полная положительная автокорреляция и =1, то d = 0. Если в остатках полная отрицательная автокор­реляция и 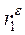= -1, то d = 4.

Таким образом, величина d изменяется в пределах

0£ d £4.

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина - Уотсона коротко состоит в следующем.

Выдвигается гипотеза H_о об от­сутствии автокорреляции остатков. Альтернативные гипотезы Н₁ и Н₁* при этом состоят соответственно в наличии положительной или отрица­тельной автокорреляции в остатках.

Далее по специальным таблицам (прил. 1 и 2) определя­ются критические значения критерия Дарбина - Уотсона d_L и d_U для заданного числа наблюдений n, числа независимых переменных мо­дели k и уровня значимости g.

По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Схема принятия решения по вопросу о допуске или отклонении каждой из гипотез с вероятностью (1 - g) рассматривается на риc.1.

Рис.1. Механизм проверки гипотезы о наличии автокорреляции

остатков

Если фактическое значение критерия Дарбина - Уотсона попадает в зону неопределенности, то нельзя сделать окончательный вывод по этому критерию.

Рассмотрим появление выбросов. График остатков хорошо показывает и резко откло­няющиеся от модели наблюдения - выбросы. Подобным аномальным наблюдениям надо уделять особо пристальное внимание, так как их присутствие может грубо искажать значения оценок. Устранение эф­фектов выбросов может проводиться либо с помощью удаления этих точек из анализируемых данных (эта процедура называется цензурированием), либо с помощью применения методов оценивания пара­метров, устойчивых к подобным грубым отклонениям.

Кроме рассмотренных характеристик, целесообразно использовать коэффициент множественной корреляции - индекс корреляции R, а также характеристики существенности модели в целом и отдельных ее коэффициентов

,

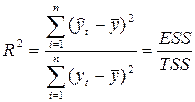где TSS - общая сумма квадратов отклонений;

ESS - сумма квадратов отклонений, объясненная регрессией.

Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции.

Коэффициент множественной корреляции (индекс корреляции), возведенный в квадрат R², называемый коэффициентом детерминации, показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов. Он определяет, какая доля вариации признака Y учтена в модели и обусловлена влияни­ем на него факторов.

В многофакторной регрессии добавление дополнительных факторных переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных.

Скорректированный R², или рассчитывается следующим образом:

,

где n - число наблюдений;

к - число независимых переменных.

В качестве оценки меры точности модели применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет со­бой отношение суммы квадратов уровней остаточной компоненты к величине (n-к-1), где k – число факторов, включенных в модель. Квадратный корень из этой величины называется стандартной ошибкой оценки.