
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обчислити дивергенцію поля в точці . 6 страница
7.3.80. Обчислити 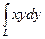 , де
, де  – контур трикутника, що обмежений осями координат і прямою
– контур трикутника, що обмежений осями координат і прямою  , який проходять проти годинникової стрілки.
, який проходять проти годинникової стрілки.
а) 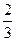 ; б)
; б) 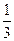 ; в)
; в) 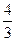 ; г) 1; д) інша відповідь.
; г) 1; д) інша відповідь.
7.3.81. Обчислити  , де
, де  – контур трикутника, що обмежений осями координат і прямою
– контур трикутника, що обмежений осями координат і прямою  , який проходять проти годинникової стрілки.
, який проходять проти годинникової стрілки.
а) -1; б) -2; в) -3; г) -4; д) інша відповідь.
7.3.82. Обчислити  , де
, де  – контур трикутника, що обмежений осями координат і прямою
– контур трикутника, що обмежений осями координат і прямою  , який проходять проти годинникової стрілки.
, який проходять проти годинникової стрілки.
а) 1; б) 2; в) 3; г) 4; д) інша відповідь.
7.3.83. Обчислити 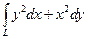 , де
, де  – дуга параболи
– дуга параболи 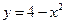 , що знаходиться у верхній півплощині і яку проходять за годинниковою стрілкою.
, що знаходиться у верхній півплощині і яку проходять за годинниковою стрілкою.
а) 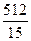 ; б)
; б) 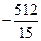 ; в) 0; г) 80; д) інша відповідь.
; в) 0; г) 80; д) інша відповідь.
7.3.84. Обчислити 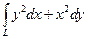 , де
, де  – ламана АВC, що з’єднує точки А(-2;0), В(0;4), C(2;0).
– ламана АВC, що з’єднує точки А(-2;0), В(0;4), C(2;0).
а) 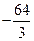 ; б)
; б)  ; в)
; в)  ; г)
; г) 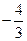 ; д) інша відповідь.
; д) інша відповідь.
7.3.85. Обчислити 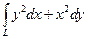 , де
, де  – відрізок прямої від точки А(-2;0) до точки B(2;0).
– відрізок прямої від точки А(-2;0) до точки B(2;0).
а) 1; б) 2; в) 3; г) 0; д) інша відповідь.
7.3.86. Обчислити  , де
, де  – дуга параболи
– дуга параболи  від точки А(0;0) до точки B(1;1).
від точки А(0;0) до точки B(1;1).
а) 1; б) 2; в) 3; г) 4; д) інша відповідь.
7.3.87. Обчислити  , де
, де  – дуга параболи
– дуга параболи 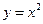 від точки А(0;0) до точки B(1;1).
від точки А(0;0) до точки B(1;1).
а) 1; б) 2; в) 3; г) 4; д) інша відповідь.
7.3.88. Обчислити  , де
, де  – відрізок прямої від точки А(0;0) до точки B(1;1).
– відрізок прямої від точки А(0;0) до точки B(1;1).
а) 1; б) 2; в) 3; г) 4; д) інша відповідь.
7.3.89. Обчислити  , де
, де  – відрізок прямої
– відрізок прямої 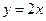 від точки А(0;0) до точки B(1;2).
від точки А(0;0) до точки B(1;2).
а) 1; б) 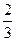 ; в)
; в) 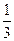 ; г) 3; д) інша відповідь.
; г) 3; д) інша відповідь.
7.3.90. Обчислити  , де
, де  – дуга параболи
– дуга параболи 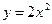 від точки А(0;0) до точки B(1;2).
від точки А(0;0) до точки B(1;2).
а) 1; б) 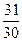 ; в)
; в)  ; г)
; г) 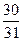 ; д) інша відповідь.
; д) інша відповідь.
7.3.91. Обчислити  , де
, де  – дуга параболи
– дуга параболи  від точки А(0;0) до точки B(1;2).
від точки А(0;0) до точки B(1;2).
а)  ; б)
; б) 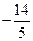 ; в)
; в) 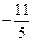 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
7.3.92. Обчислити  , де
, де  – ламана АВC: А(0;0), В(2;0), C(4;5).
– ламана АВC: А(0;0), В(2;0), C(4;5).
а) 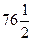 ; б) 10,5; в) 132; г)
; б) 10,5; в) 132; г) 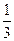 ; д) інша відповідь.
; д) інша відповідь.
7.3.93. Обчислити 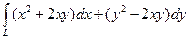 , де
, де  – дуга параболи
– дуга параболи 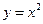 від точки А(-1;1) до точки B(1;1).
від точки А(-1;1) до точки B(1;1).
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
7.3.94. Обчислити 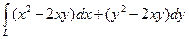 , де
, де  – дуга параболи
– дуга параболи 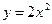 від точки А(-1;2) до точки B(1;2).
від точки А(-1;2) до точки B(1;2).
а)  ; б)
; б)  ; в)
; в) 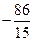 ; г)
; г) 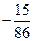 ; д) інша відповідь
; д) інша відповідь
7.3.95. Обчислити 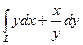 , де
, де  – дуга кривої
– дуга кривої 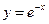 від точки А(0;1) до точки B(-1;e).
від точки А(0;1) до точки B(-1;e).
а)  ; б)
; б) 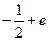 ; в)
; в)  ; г)
; г) 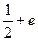 ;
;
д) інша відповідь.
7.3.96. Обчислити 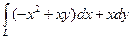 , де
, де  – дуга параболи
– дуга параболи 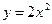 від точки А(0;0) до точки B(1;2).
від точки А(0;0) до точки B(1;2).
а)  ; б)
; б)  ; в)
; в) 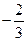 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
7.3.97. Обчислити 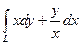 , де
, де  – дуга кривої
– дуга кривої  від точки А(1;0) до точки B(e;1).
від точки А(1;0) до точки B(e;1).
а) e; б)  ; в)
; в) 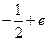 ; г) 1+e; д) інша відповідь.
; г) 1+e; д) інша відповідь.
7.3.98. Обчислити 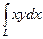 , де
, де  – дуга синусоїди від точки А(
– дуга синусоїди від точки А(  ;0) до точки В(0;0).
;0) до точки В(0;0).
а) 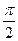 ; б)
; б)  ; в) 2
; в) 2  ; г)
; г)  +1; д) інша відповідь.
+1; д) інша відповідь.
7.3.99. Обчислити 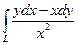 , де
, де  – відрізок прямої від точки А(2;1) до точки В(1;2).
– відрізок прямої від точки А(2;1) до точки В(1;2).
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 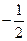 ; д) інша відповідь.
; д) інша відповідь.
7.3.100. Обчислити  , де
, де  – крива:
– крива:  .
.
а) 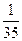 ; б)
; б) 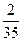 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
7.3.101. Обчислити  , де σ – поверхня частини площини x+2y+3z=6, що розміщена в першому октанті.
, де σ – поверхня частини площини x+2y+3z=6, що розміщена в першому октанті.
а) 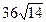 ; б)
; б)  ; в)
; в) 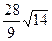 ; г)
; г)  ;
;
д) інша відповідь.
7.1 Теоретичні питання
7.1.1. Подвійний інтеграл. Означення та властивості.
7.1.2. Обчислення подвійних інтегралів в декартових координатах.
7.1.3. Заміна змінних у подвійному інтегралі. Подвійний інтеграл в полярних координатах.
7.1.4. Геометричні та фізичні застосування подвійних інтегралів.
7.1.5. Потрійний інтеграл. Означення та властивості.
7.1.6. Обчислення потрійних інтегралів в декартових координатах.
7.1.7. Заміна змінних у потрійному інтегралі. Потрійний інтеграл в циліндричних та сферичних координатах.
7.1.8. Застосування потрійних інтегралів.
7.1.9. Криволінійний інтеграл першого роду. Означення та властивості.
7.1.10. Обчислення криволінійних інтегралів першого роду.
7.1.11. Криволінійний інтеграл другого роду. Означення та властивості.
7.1.12. Обчислення криволінійних інтегралів другого роду.
7.1.13. Застосування криволінійних інтегралів першого і другого роду.
7.1.14. Поверхневий інтеграл першого роду. Означення та властивості.
7.1.15. Обчислення поверхневих інтегралів першого роду.
7.1.16. Поверхневий інтеграл другого роду. Означення та властивості.
7.1.17. Обчислення поверхневих інтегралів другого роду.
7.1.18. Взаємозв’язок між криволінійними інтегралами першого та другого роду та між поверхневими інтегралами першого та другого роду.
7.1.19. Застосування поверхневих інтегралів першого і другого роду.
7.1.20. Формула Гріна.
7.1.21. Умови незалежності криволінійного інтеграла від форми шляху інтегрування.
7.1.22. Формула Стокса.
7.1.23. Формула Остроградського-Гаусса.
7.1.24. Потік векторного поля через поверхню. Дивергенція.
7.1.25. Циркуляція векторного поля. Ротор.
7.1.26. Потенціальне поле.
Дата добавления: 2014-12-30; просмотров: 306; Мы поможем в написании вашей работы!; Нарушение авторских прав |