
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тестові теоретичні завдання. 7.2.1. Які з наведених нижче тверджень є правильними?
7.2.1. Які з наведених нижче тверджень є правильними?
1) Обмеженість функції  в обмеженій замкненій області
в обмеженій замкненій області 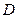 є достатньою умовою її інтегровності в цій області.
є достатньою умовою її інтегровності в цій області.
2) Неперервність функції  в обмеженій замкненій області
в обмеженій замкненій області 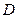 є достатньою умовою її інтегровності в цій області.
є достатньою умовою її інтегровності в цій області.
3) Обмеженість функції  в обмеженій замкненій області
в обмеженій замкненій області 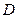 є необхідною умовою її інтегровності в цій області.
є необхідною умовою її інтегровності в цій області.
4) Неперервність функції  в обмеженій замкненій області
в обмеженій замкненій області 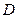 є необхідною умовою її інтегровності в цій області.
є необхідною умовою її інтегровності в цій області.
а) 1 і 4; б) 2 і 3; в) тільки 3;
г) тільки 4; д) інша відповідь.
7.2.2. Які з наведених нижче тверджень є правильними?
1) Якщо функція  інтегровна в області
інтегровна в області 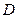 , то вона неперервна в цій області.
, то вона неперервна в цій області.
2) Якщо функція  інтегровна в обмеженій замкненій області
інтегровна в обмеженій замкненій області  , то вона обмежена в цій області.
, то вона обмежена в цій області.
3) Для того, щоб функція  була інтегровною в області
була інтегровною в області  необхідно і достатньо, щоб область була обмеженою і замкненою, а функція – обмеженою в цій області.
необхідно і достатньо, щоб область була обмеженою і замкненою, а функція – обмеженою в цій області.
4) Якщо функція неперервна в обмеженій замкненій області  , то вона інтегровна в цій області.
, то вона інтегровна в цій області.
а) тільки 2; б) тільки 3; в) 2 і 4;
г) 3 і 4; д) інша відповідь.
7.2.3. Які з наведених нижче тверджень не є правильними ?
1) Для того, щоб функція  була інтегровною в області
була інтегровною в області  необхідно, щоб вона була неперервною в цій області.
необхідно, щоб вона була неперервною в цій області.
2) Для того, щоб функція  була інтегровною в області
була інтегровною в області  необхідно, щоб вона була обмеженою в цій області.
необхідно, щоб вона була обмеженою в цій області.
3) Для того, щоб функція  була інтегровною в області
була інтегровною в області  достатньо, щоб вона була обмеженою в цій області.
достатньо, щоб вона була обмеженою в цій області.
4) Для того, щоб функція  була інтегровною в області
була інтегровною в області  достатньо, щоб область була обмеженою і замкненою, а функція була неперервною в цій області.
достатньо, щоб область була обмеженою і замкненою, а функція була неперервною в цій області.
а) 2 і 3; б) тільки 1; в) 1 і 3;
г) тільки 2; д) інша відповідь.
7.2.4. Які з наведених нижче тверджень не є правильними ?
1) Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області  необхідно і достатньо, щоб функція була неперервною в цій області.
необхідно і достатньо, щоб функція була неперервною в цій області.
2) Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області  необхідно, щоб функція була обмеженою в цій області.
необхідно, щоб функція була обмеженою в цій області.
3) Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області  достатньо, щоб вона була неперервною в цій області.
достатньо, щоб вона була неперервною в цій області.
4) Для того, щоб функція  була інтегровною в обмеженій замкненій області
була інтегровною в обмеженій замкненій області  достатньо, щоб вона була обмеженою в цій області.
достатньо, щоб вона була обмеженою в цій області.
а) 1 і 4; б) 2 і 3; в) тільки 1;
г) 2 і 4; д) інша відповідь.
7.2.5. Які з наведених нижче рівностей справедливі для подвійного інтеграла ?
1) 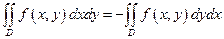 ;
;
2)  ;
;
3)  ;
;
4)  (
(  ).
).
а) 2 і 3; б) тільки 3; в) 2 і 4;
г) 3 і 4; д) інша відповідь.
7.2.6. Які з наведених нижче тверджень справедливі для подвійного інтеграла ?
1) Якщо в області  функція
функція  , то
, то  ;
;
2) Якщо область  , причому
, причому 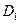 і
і  не мають спільних внутрішніх точок, то
не мають спільних внутрішніх точок, то  ;
;
3) Для довільних обмежених замкнених областей 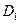 і
і  справедлива рівність
справедлива рівність  ;
;
4)  , де
, де  - площа області
- площа області  .
.
а) 1, 2 і 4; б) 1, 2 і 3; в) 1 і 2;
г) всі; д) інша відповідь.
7.2.7. Якщо 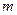 і
і  - відповідно найменше і найбільше значення функції
- відповідно найменше і найбільше значення функції  в області
в області  , а
, а  - площа цієї області, то має місце оцінка подвійного інтеграла:
- площа цієї області, то має місце оцінка подвійного інтеграла:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
7.2.8. Середнім значенням функції  в області
в області  називається величина (
називається величина (  - площа області
- площа області  ):
):
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 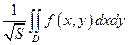 ;
;
д) інша відповідь.
7.2.9. За якою формулою можна обчислити площу плоскої фігури  ?
?
а)  ; б)
; б)  ; в)
; в) 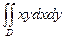 ; г)
; г)  ;
;
д) інша відповідь.
7.2.10. Які з наведених нижче формул не можуть бути правильними ?
1)  ;
;
2)  ;
;
3) 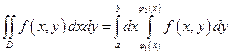 ;
;
4)  .
.
а) 1 і 2; б) 2, 3 і 4; в) 2 і 4;
г) всі; д) інша відповідь.
7.2.11. Які з наведених нижче формул не можуть бути правильними ?
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
а) 1, 2 і 3; б) 1, 2 і 4; в) 1 і 3;
г) 2 і 3; д) інша відповідь.
7.2.12. Які з наведених нижче формул є правильними ?
1)  ;
;
2) 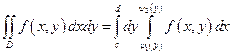 ;
;
3) 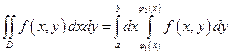 ;
;
4)  .
.
а) 1, 2 і 3; б) тільки 3; в) 2 і 3;
г) 2 і 4; д) інша відповідь.
7.2.13. Які з наведених нижче формул є правильними ?
1)  ;
;
2)  ;
;
3)  ;
;
4) 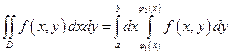 .
.
а) 1 і 4; б) 2 і 3; в) 2 і 4;
г) тільки 4; д) інша відповідь.
7.2.14. Які з наведених нижче формул є правильними ?
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
а) 2 і 3; б) 1 і 4; в) 3 і 4;
г) тільки 4; д) інша відповідь.
7.2.15. Подвійний інтеграл  в полярних координатах
в полярних координатах  набуває виду:
набуває виду:
а)  ;
;
б) 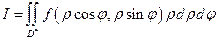 ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.16. Якщо поверхня  задана рівнянням
задана рівнянням  і проектується на площину
і проектується на площину 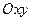 в область
в область  , то її площа
, то її площа  знаходиться за формулою:
знаходиться за формулою:
а)  ;
;
б) 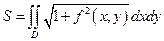 ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.17. Маса матеріальної пластини, яка займає область  на площині і поверхнева густина якої
на площині і поверхнева густина якої  , обчислюється за формулою:
, обчислюється за формулою:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
7.2.18. Координати центра ваги матеріальної пластини, яка займає область  на площині і поверхнева густина якої
на площині і поверхнева густина якої  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.19. Моменти інерції матеріальної пластини, яка займає область  на площині і поверхнева густина якої
на площині і поверхнева густина якої  , відносно координатних осей і відносно початку координат обчислюються за формулами:
, відносно координатних осей і відносно початку координат обчислюються за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.20. Які з наведених нижче рівностей справедливі для потрійного інтеграла?
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
а) 1 і 2; б) тільки 4; в) 1 і 4;
г) 2 і 3; д) інша відповідь.
7.2.21. Які з наведених нижче формул не можуть бути правильними ?
1)  ;
;
2) 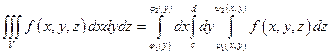 ;
;
3) 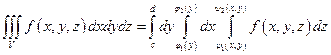 ;
;
4)  .
.
а) тільки 2; б) 2 і 4; в) 3 і 4;
г) 2 і 3; д) інша відповідь.
7.2.22. Які з наведених нижче формул не можуть бути правильними ?
1) 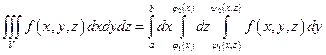 ;
;
2) 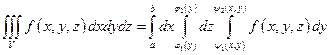 ;
;
3)  ;
;
4)  .
.
а) тільки 3; б) 1 і 2; в) 2 і 4;
г) 2 і 3; д) інша відповідь.
7.2.23. Які з наведених нижче формул є правильними ?
1)  (
(  - проекція
- проекція 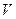 на площину
на площину 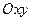 );
);
2)  ;
;
3)  ;
;
4)  (
(  - проекція
- проекція 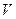 на площину
на площину  ).
).
а) 1 і 4; б) тільки 3; в) 1 і 3;
г) 2 і 3; д) інша відповідь.
7.2.24. Які з наведених нижче формул є правильними ?
1)  (
(  - проекція
- проекція 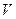 на площину
на площину 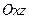 );
);
2)  ;
;
3)  ;
;
4)  (
(  - проекція
- проекція 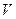 на площину
на площину 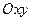 ).
).
а) 1 і 4; б) тільки 1; в) 2 і 3;
г) 2 і 4; д) інша відповідь.
7.2.25. Потрійний інтеграл 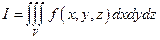 в циліндричних координатах
в циліндричних координатах  набуває виду:
набуває виду:
а) 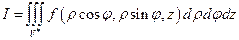 ;
;
б) 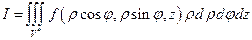 ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.26. Потрійний інтеграл 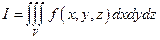 в сферичних координатах
в сферичних координатах  набуває виду:
набуває виду:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.27. Маса тіла 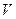 , густина якого
, густина якого  , обчислюється за формулою:
, обчислюється за формулою:
а)  ; б)
; б)  ;
;
в) 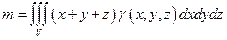 ;
;
г) 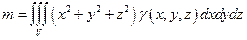 ;
;
д) інша відповідь.
7.2.28. Координати центра ваги тіла 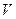 , густина якого
, густина якого  , знаходяться за формулами (
, знаходяться за формулами ( 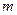 - маса тіла):
- маса тіла):
а) 
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.29. Моменти інерції відносно координатних осей тіла 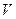 , густина якого
, густина якого  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.30. Моменти інерції відносно координатних площин тіла 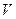 , густина якого
, густина якого  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.31. Момент інерції відносно початку координат тіла 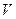 , густина якого
, густина якого  , знаходиться за формулою:
, знаходиться за формулою:
а) 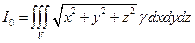 ; б)
; б)  ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.32. Які з наведених нижче рівностей справедливі для криволінійного інтеграла першого роду ?
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
а) 3 і 4; б) 1, 2, і 4; в) тільки 1;
г) 1 і 4; д) інша відповідь.
7.2.33. Які з наведених нижче рівностей справедливі для криволінійного інтеграла першого роду ?
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
а) 1 і 3; б) 2 і 3; в) 1, 3 і 4 ;
г) тільки 2; д) інша відповідь.
7.2.34. Якщо крива 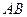 задана рівнянням
задана рівнянням  , то для обчислення криволінійного інтеграла першого роду має місце формула:
, то для обчислення криволінійного інтеграла першого роду має місце формула:
а) 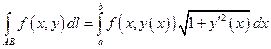 ;
;
б)  ;
;
в)  ;
;
г) 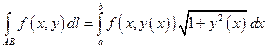 ;
;
д) інша відповідь.
7.2.35. Якщо крива 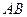 задана рівнянням
задана рівнянням  , то для обчислення криволінійного інтеграла першого роду має місце формула:
, то для обчислення криволінійного інтеграла першого роду має місце формула:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.36. Якщо крива 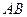 задана параметричними рівняннями
задана параметричними рівняннями  , то для обчислення криволінійного інтеграла першого роду має місце формула:
, то для обчислення криволінійного інтеграла першого роду має місце формула:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.37. Якщо просторова крива 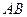 задана параметричними рівняннями
задана параметричними рівняннями 
 , то для обчислення криволінійного інтеграла першого роду має місце формула:
, то для обчислення криволінійного інтеграла першого роду має місце формула:
а)  ;
;
б)  ;
;
в) 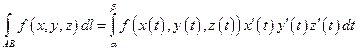 ;
;
г)  ;
;
д) інша відповідь.
7.2.38. Довжина кривої 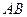 обчислюється за формулою:
обчислюється за формулою:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.39. Маса плоскої матеріальної кривої 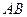 , лінійна густина якої
, лінійна густина якої  , обчислюється за формулою:
, обчислюється за формулою:
а) 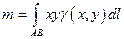 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
7.2.40. Координати центра ваги плоскої матеріальної кривої 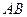 , лінійна густина якої
, лінійна густина якої  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в) 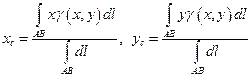 ;
;
г)  ;
;
д) інша відповідь.
7.2.41. Моменти інерції відносно координатних осей і відносно початку координат плоскої матеріальної кривої 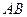 , лінійна густина якої
, лінійна густина якої  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.42. Які з наведених нижче рівностей справедливі для криволінійного інтеграла другого роду?
1) 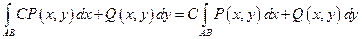
(  );
);
2)  ;
;
3) 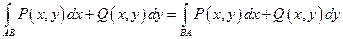 ;
;
4)  .
.
а) 1 і 2; б) 1, 2 і 4; в) 2 і 3;
г) тільки 4; д) інша відповідь.
7.2.43. Якщо крива 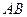 задана рівнянням
задана рівнянням  , то для обчислення криволінійного інтеграла другого роду має місце формула:
, то для обчислення криволінійного інтеграла другого роду має місце формула:
а)  ;
;
б) 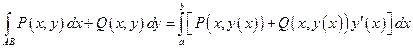 ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.44. Якщо крива 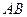 задана рівнянням
задана рівнянням  , то для обчислення криволінійного інтеграла другого роду має місце формула:
, то для обчислення криволінійного інтеграла другого роду має місце формула:
а)  ;
;
б) 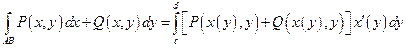 ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.45. Якщо крива 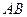 задана параметричними рівняннями
задана параметричними рівняннями  , то для обчислення криволінійного інтеграла другого роду має місце формула:
, то для обчислення криволінійного інтеграла другого роду має місце формула:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.46. Зв’язок між криволінійними інтегралами першого і другого роду. Якщо  і
і  - кути, які складає напрямна дотична до кривої
- кути, які складає напрямна дотична до кривої 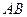 з осями відповідно
з осями відповідно  і
і  , то має місце рівність:
, то має місце рівність:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.47. Формула Гріна встановлює зв’язок між:
а) криволінійними інтегралами першого і другого роду;
б) подвійними і криволінійними інтегралами;
в) криволінійними і поверхневими інтегралами;
г) подвійними і потрійними інтегралами;
д) інша відповідь.
7.2.48. Формула Гріна має вид ( 
 - замкнений контур, що обмежує область
- замкнений контур, що обмежує область  і обходиться в додатному напрямі):
і обходиться в додатному напрямі):
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.49. Яка з формул для обчислення площі області  , обмеженої контуром
, обмеженої контуром  не є правильною ?
не є правильною ?
а)  ; б)
; б) 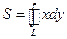 ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.50. Інтеграл  не залежить від форми шляху інтегрування, якщо виконана умова:
не залежить від форми шляху інтегрування, якщо виконана умова:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) інша відповідь.
7.2.51. Інтеграл  не залежить від форми шляху інтегрування, якщо виконані умови:
не залежить від форми шляху інтегрування, якщо виконані умови:
а)  ;
;
б)  ;
;
в) 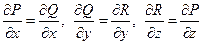 ;
;
г)  ;
;
д) інша відповідь.
7.2.52. Якщо поверхня  задана рівнянням
задана рівнянням  і проектується на площину
і проектується на площину 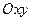 в область
в область  , то для обчислення поверхневого інтеграла першого роду має місце формула:
, то для обчислення поверхневого інтеграла першого роду має місце формула:
а)  ;
;
б)  ;
;
в)  ;
;
г) 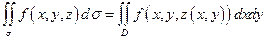 ;
;
д) інша відповідь.
7.2.53. Якщо поверхня  задана рівнянням
задана рівнянням  і проектується на площину
і проектується на площину  в область
в область  , то для обчислення поверхневого інтеграла першого роду має місце формула:
, то для обчислення поверхневого інтеграла першого роду має місце формула:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.54. Якщо поверхня  задана рівнянням
задана рівнянням  і проектується на площину
і проектується на площину  в область
в область  , то для обчислення поверхневого інтеграла першого роду має місце формула:
, то для обчислення поверхневого інтеграла першого роду має місце формула:
а)  ;
;
б) 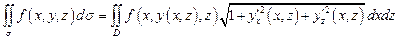 ;
;
в) 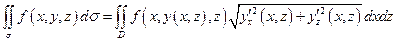 ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.55. Площу поверхні  можна обчислити за формулою:
можна обчислити за формулою:
а)  ; б)
; б)  ; в)
; в)  ;
;
г) 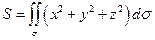 ; д) інша відповідь.
; д) інша відповідь.
7.2.56. Маса матеріальної поверхні  , поверхнева густина якої
, поверхнева густина якої  , знаходиться за формулою:
, знаходиться за формулою:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) інша відповідь.
7.2.57. Координати центра ваги матеріальної поверхні  , поверхнева густина якої
, поверхнева густина якої  , знаходяться за формулами (
, знаходяться за формулами ( 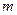 - маса поверхні):
- маса поверхні):
а)  ;
;
б) 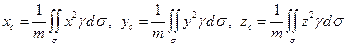 ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.58. Моменти інерції відносно координатних осей матеріальної поверхні  , поверхнева густина якої
, поверхнева густина якої  , знаходяться за формулами:
, знаходяться за формулами:
а)  ;
;
б)  ;
;
в)  ;
;
г) 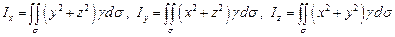 ;
;
д) інша відповідь.
7.2.59. Момент інерції відносно початку координат матеріальної поверхні  , поверхнева густина якої
, поверхнева густина якої  , знаходиться за формулою:
, знаходиться за формулою:
а) 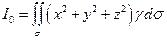 ; б)
; б)  ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.60. Зв’язок між поверхневими інтегралами першого і другого роду. Якщо 

 - функції, задані в точках поверхні
- функції, задані в точках поверхні  ,
,  - кути між нормаллю до вибраної сторони поверхні
- кути між нормаллю до вибраної сторони поверхні  та осями
та осями  відповідно, то має місце рівність:
відповідно, то має місце рівність:
а)  ;
;
б)  ;
;
в) 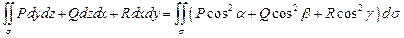 ;
;
г)  ;
;
д) інша відповідь.
7.2.61. Формула Остроградського-Гаусса встановлює зв’язок між:
а) поверхневими інтегралами першого і другого родів;
б) подвійними і поверхневими інтегралами;
в) криволінійними і поверхневими інтегралами;
г) потрійними і поверхневими інтегралами;
д) інша відповідь.
7.2.62. Формула Остроградського-Гаусса має вид ( 
 ,
,  - замкнена поверхня, що обмежує область
- замкнена поверхня, що обмежує область 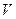 ):
):
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) інша відповідь.
7.2.63. Формула Стокса встановлює зв’язок між:
а) криволінійними і поверхневими інтегралами;
б) криволінійними і потрійними інтегралами;
в) подвійними і криволінійними інтегралами;
г) подвійними і потрійними інтегралами;
д) інша відповідь.
7.2.64. Формула Стокса має вид ( 

 ,
,  - замкнений контур, що обмежує поверхню
- замкнений контур, що обмежує поверхню  ):
):
а)  ;
;
б)  ;
;
в)  ;
;
г) 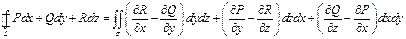 ;
;
д) інша відповідь.
7.2.65. Робота сили  по переміщенню матеріальної точки вздовж кривої
по переміщенню матеріальної точки вздовж кривої  дорівнює:
дорівнює:
а)  ; б)
; б)  ;
;
в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.66. Потік вектора 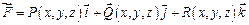 через поверхню
через поверхню  знаходиться за формулою:
знаходиться за формулою:
а) П  ;
;
б) П  ;
;
в) П  ;
;
г) П  ; д) інша відповідь.
; д) інша відповідь.
7.2.67. Циркуляція вектора 
 вздовж замкненого контура
вздовж замкненого контура  знаходиться за формулою:
знаходиться за формулою:
а) Ц  ; б) Ц
; б) Ц  ;
;
в) Ц  ;
;
г) Ц  ; д) інша відповідь.
; д) інша відповідь.
7.2.68. Градієнтом скалярного поля  називається:
називається:
а) скаляр  ;
;
б) вектор  ;
;
в) вектор  ;
;
г) скаляр  ;
;
д) інша відповідь.
7.2.69. Дивергенцією векторного поля  називається:
називається:
а) вектор  ;
;
б) скаляр  ;
;
в) вектор  ;
;
г) скаляр  ;
;
д) інша відповідь.
7.2.70. Ротором векторного поля  називається:
називається:
а) вектор  ;
;
б) вектор  ;
;
в) вектор  ;
;
г) скаляр  ;
;
д) інша відповідь.
7.2.71. Векторне поле 
 називається соленоїдальним, якщо:
називається соленоїдальним, якщо:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
7.2.72. Векторне поле 
 буде потенціальним, якщо:
буде потенціальним, якщо:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) Існує таке скалярне поле  , що
, що  .
.
З наведених тверджень правильними є:
а) 1 і 4; б) 2 і 4; в) 2 і 3;
г) тільки 2; д) інша відповідь.
7.2.73. Які з наведених нижче рівностей є правильними (  ,
,  )?
)?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
а) 1 і 2; б) 3 і 4; в) 1, 2 і 3;
г) тільки 2; д) інша відповідь.
7.2.74. Які з наведених нижче рівностей є правильними ( 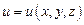 ,
,  )?
)?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
а) 1 і 2; б) 3 і 4; в) тільки 1;
г) 1 і 4; д) інша відповідь.
7.2.75. Які з наведених нижче рівностей є правильними (  ,
,  )?
)?
1) 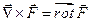 ; 2)
; 2)  ;
;
3) 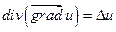 ; 4)
; 4)  .
.
а) 1 і 2; б) 1 і 3; в) 3 і 4;
г) тільки 1; д) інша відповідь.
Дата добавления: 2014-12-30; просмотров: 351; Мы поможем в написании вашей работы!; Нарушение авторских прав |