
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № 3
«Интегрирование»
(2-ой семестр)
Вариант 1
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) ;б)
;б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной параболой у = 3x2 + 1 и прямой у = 3x + 7.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)3 = а2 х2 у2.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = x, y = 0, y = 4, x =  .
.
Задание 7.
Вычислить криволинейный интеграл

вдоль дуги 1 окружности x = 5 cos t, y = 5 sin2 t, обходя ее против хода часовой стрелки от точки А (5; 0) до точки В (0; 5). Сделать чертеж.
Вариант 2
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)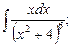 б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.
.
Задание 4.
Вычислить площадь фигуры, ограниченной одной аркой циклоиды x = a (t – sin t); y = a (1-cos t); (  ) и осью Ox.
) и осью Ox.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = а2 (4х2+ у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 9 – у2, x2 + у2 = 9.
Задание 7.
Вычислить криволинейный интеграл
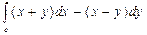
вдоль ломанной 1 = ОАВ, где О (0; 0); А (2; 0); В (4; 5). Сделать чертеж.
Вариант 3
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в) 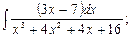 г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной кардиоидой r = 3 (1 + cos  ).
).
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)3 = а2 х2 (4х2+3у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 4 – х – у , x2 + у2 = 4.
Задание 7.
Вычислить криволинейный интеграл

вдоль границы  , обходя ее против хода часовой стрелки, если А (1; 0); В (1; 1); С (0; 1). Сделать чертеж.
, обходя ее против хода часовой стрелки, если А (1; 0); В (1; 1); С (0; 1). Сделать чертеж.
Вариант 4
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в) 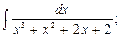 г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной четырехлепестковой розойr = 4 sin 2  .
.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = а2 (3х2+ у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = у2 , x2 + у2 = 9.
Задание 7.
Вычислить криволинейный интеграл

вдоль дуги 1 параболы у = х2 от точки А (-1; 1) до точки В (1; 1). Сделать чертеж.
Вариант 5
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить объем тела, образованного вращением вокруг оси Оx фигуры, ограниченной параболами у = х2 и у =  .
.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х4 = а2 (3х2- у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, у + z = 4, x2 + у2 = 4.
Задание 7.
Вычислить криволинейный интеграл

вдоль верхней половины 1 эллипса х = 3 cos t, у = 2 sin t, (  ).
).
Вариант 6
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченном полуэллипсом у = 3 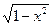 , параболой х =
, параболой х =  и осью Оу.
и осью Оу.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х6 = а2 (х4- у4).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, 4z = у2, 2x - у = 0, х + у = 9.
Задание 7.
Вычислить криволинейный интеграл

вдоль ломанной t = ABC, где А (1; 2); В (1; 5); С (3; 5). Сделать чертеж.
Вариант 7
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2 / (1+x2) и у = x2.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х4 = а2 ( х2 - 3 у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, х2 + у2 = z, x2 + у2 = 4.
Задание 7.
Вычислить криволинейный интеграл

вдоль дуги 1 кривой у = е-х от точки А (0; 1) до точки В (-1; е). Сделать чертеж.
Вариант 8
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 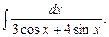
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
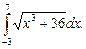
Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину дуги полукубической параболы у =  от точки А (2; 0) до точки В (6; 8).
от точки А (2; 0) до точки В (6; 8).
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
у6 = а2 (у4 – х4).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 1 – у2, x = у2, х = 2у2 + 1.
Задание 7.
Вычислить криволинейный интеграл

вдоль отрезка t = AB прямой от точки А (1; 2) до точки В (2; 4). Сделать чертеж.
Вариант 9
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) 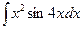 ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину кардиоиды r = 3 (1 – cos  ).
).
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = а2 (2х2+3у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 1 – х2, у = 0, у = 3 – х.
Задание 7.
Вычислить криволинейный интеграл

вдоль дуги t параболы у = 2х2 от точки О (0; 0) до точки А (1; 2). Сделать чертеж.
Вариант 10
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину одной арки циклоиды x = 3 (t – sin t); y = 3 (1- cos t); (  ).
).
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
у6 = а2 (х2 + у2)(3у2 – х2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 4  , x = 0, х + у = 4.
, x = 0, х + у = 4.
Задание 7.
Вычислить криволинейный интеграл

вдоль дуги 1 кривой у = ln x от точки А (1; 0) до точки В (е; 1). Сделать чертеж.
Вариант 11
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной параболой у = -х2 – 4 и прямой 2х – у + 1 = 0.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = 2а х3.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 2х, x + у = 3, х =  .
.
Задание 7.
Вычислить криволинейный интеграл

где С есть верхняя половина эллипса х = а cos t, y = b sin t, пробегаемая против хода часовой стрелки.
Вариант 12
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) 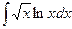 ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной гиперболой ху = 1, ветвью параболы у = х2, находящейся в первом квадранте, и прямой у = 4.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = 2а2 (х2 - у2).
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, x + у = 2, у = 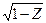 .
.
Задание 7.
Вычислить криволинейный интеграл

где С есть треугольник с вершинами в точках О (0; 0); А (1; 0); В (0; 1), пробегаемый против хода часовой стрелки.
Вариант 13
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)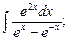 б)
б)  ; в)
; в) 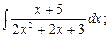 г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить площадь фигуры, ограниченной астроидой 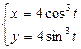 .
.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = 2а2 ху.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 1 – у, у = х2.
Задание 7.
Вычислить криволинейный интеграл

где С есть дуга параболы у2 = х от точки А (1; 1) до точки В (4; 2).
Вариант 14
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в) 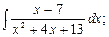 г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2 – х4 и у = х2.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х3 + у3 = аху.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 2 – х, x = 1, х = у2.
Задание 7.
Вычислить криволинейный интеграл
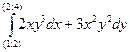
вдоль любого пути, соединяющего точки (1; 2) и (2; 4).
Вариант 15
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной полуэллипсом 2у = 3  и параболой 4у = 4 – х2.
и параболой 4у = 4 – х2.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)5 = а6 ху3.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, x + у = 1, z = x2 + 3y2.
Задание 7.
Вычислить криволинейный интеграл

где С есть окружность x = R cos t, y = R sin t, пробегаемая по ходу часовой стрелки.
Вариант 16
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину дуги полукубической параболы у = х3/2 от х = 0 до х = 5.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)5 = а4 х4 у2.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, x = 1, х + у = 2, z = x2 +  y2.
y2.
Задание 7.
Вычислить криволинейный интеграл

по любому пути, соединяющему точки (0; 0) и (3; 4).
Вариант 17
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)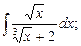 б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.
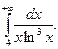
Задание 4.
Вычислить длину кривой 2у = ех + е-х от х = 0 до х = ln3.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)3 = а4 у2.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, у + z = 1, x = y2 + 1.
Задание 7.
Вычислить криволинейный интеграл

где С есть окружность x = R cos t, y = R sin t, пробегаемая против хода часовой стрелки.
Вариант 18
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 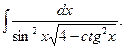
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину дуги кривой
 от t = 0 до t =
от t = 0 до t =  .
.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)3 = а4 х2.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z =  , у = x2.
, у = x2.
Задание 7.
Вычислить криволинейный интеграл

по любому пути, соединяющему точки (1; 2) и (3; 6).
Вариант 19
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) 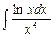 ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.
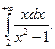
Задание 4.
Найти длину дуги гиперболической спирали  = 1 от точки А (2;1/2) до точки В (1/2; 2).
= 1 от точки А (2;1/2) до точки В (1/2; 2).
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)3 = а2(2х2 + у2).
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, z = y2, у + x = 2.
Задание 7.
Вычислить криволинейный интеграл

вдоль параболы  от точки А (0; 0) до точки В (1; 2).
от точки А (0; 0) до точки В (1; 2).
Вариант 20
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  ; в)
; в)  г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 4.
Вычислить длину дуги логарифмической спирали 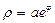 от
от  до
до 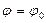 .
.
Задание 5.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)7 = а8 х4 у2.
Задание 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
х = 0, у = 0, z = 0, x = 4, у = 4, z = х2 + у2 + 1.
Задание 7.
Вычислить криволинейный интеграл

где е – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t., (  ).
).
Вариант 21
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  в)
в)  г)
г) 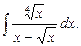
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вычислить площадь фигуры ограниченной линиями 
Задание 5.
Переходя к полярным координатам, вычислить: 
Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 22
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б)  в)
в)  г)
г)
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вычислить площадь фигуры ограниченной линией 
Задание 5.
Переходя к полярным координатам, вычислить: 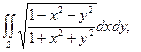

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 23
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) 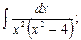 г)
г)
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Исследовать на сходимость несобственный интеграл: 
Задание 4.
Вычислить площадь фигуры ограниченной линиями 
Задание 5.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл: 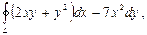 где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 24
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
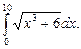
Задание 3.
Вычислить несобственный интеграл: 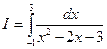 или установить его расходимость.
или установить его расходимость.
Задание 4.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 25
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл:  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вычислить площадь фигуры ограниченной линиями 
Задание 5.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:
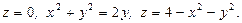
Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 26
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г)
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
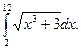
Задание 3.
Исследовать на сходимость несобственный интеграл: 
Задание 4.
Вычислить площадь фигуры, ограниченной линиями 
Задание 5.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 27
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г)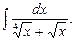
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл:  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вычислить площадь фигуры, ограниченной линиями 
Задание 5.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл:  где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 28
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г)
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл:  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вычислить площадь фигуры, ограниченной линией 
Задание 5.
Переходя к полярным координатам, вычислить: 

Задание 6.
Вычислить объем тела, ограниченного поверхностями:

Сделать чертеж данного тела и его проекции на плоскость Хоу.
Задание 7.
Пользуясь формулой Грина, вычислить криволинейный интеграл: 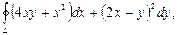 где
где  - пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:
- пробегаемый в положительном направлении (против движения часовой стрелки) контур треугольника с вершинами в точках:  Сделать чертеж.
Сделать чертеж.
Вариант 29
Задание 1.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а) б)
б) в)
в) г)
г) 
Задание 2.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 3.
Вычислить несобственный интеграл:  или установить его расходимость.
или установить его расходимость.
Задание 4.
Вы
Дата добавления: 2014-12-30; просмотров: 1232; Мы поможем в написании вашей работы!; Нарушение авторских прав |