Контрольная работа № 2 4 страница

z = x² + 2xy + 3y²; A (2; 1); B (1,96; 1,04).

Задание 10.

Дана функция u = f (x; y; z), точка А (x₀; y₀; z₀) и вектор 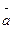(а₁; а₂; a₃). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

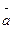u = x² + u² + z²; A (1; 1; 1); (2; 1; 3).

Вариант 23

Задание 1.

Найти производные данных функций.

а)

б)

в)

г);

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) б) .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,79, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=-1/3x³+3,5x²-10x-1/3; [-1;7].

Задание 5.

Прочность балки прямоугольного сечения пропорциональна ширине балки и квадрату ее высоты. Из бревна, диаметр которого 30 см, необходимо изготовить балку наибольшей прочности. Определить стороны прямоугольного сечения наибольшей прочности.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)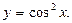

Задание 7.

Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением 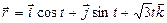в точке t = p/2.

Задание 8.

Найти полную производную сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 3x² + 2y² + xy; A (-1; 3); B (-0,98; 2,97).

Задание 10.

Дана функция u = f (x; y; z), точка А (x₀; y₀; z₀) и вектор 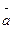(а₁; а₂; a₃). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

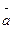u = x² + u² + z²; A (1; 1; 1); (1; 1; 1).

Вариант 24

Задание 1.

Найти производные данных функций.

а)

б)

в)

г);

д)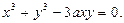

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а); б) .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,62, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=-4x³/3+2x²; [-1;3].

Задание 5.

Вычислить наименьший периметр треугольника, построенного на прямоугольной системе координат, если две его вершины имеют координаты (0;2) и (6;2), а третья лежит на оси абсцисс.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .

Задание 7.

Составить уравнение касательной и нормальной плоскости к кривой в точке t= .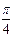

Задание 8.

Найти полную производную сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 2xy + 3y² – 5x; A (3; 4); B (3,05; 3,95).

Задание 10.

Дана функция z = f (x; y), точки А (x₀; y₀) и А₁(х₁;y₁). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .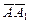

z = 5x² -3x-y-1; A (2; 1); А₁ (5; 5).

Вариант 25

Задание 1.

Найти производные данных функций.

а)

б)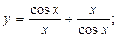

в)

г)

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

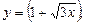а) б) .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,22, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=-x³-4x²+3x+8; [-2;3].

Задание 5.

Тело движется по закону s(t)=62,6 +54t²-0,2t⁵. В какой момент времени тело имеет наибольшую скорость? Каковы скорость и ускорение в этот момент времени? Какой путь пройдет тело до того же момента времени?

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .

Задание 7.

Составить уравнения касательной к кривой 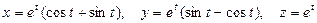в точке t=0.

Задание 8.

Найти частные производные сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = x² + 3xy + 2y² ; A (1; 3); B (1,03; 2,97).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор 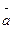(а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

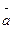z = x² – xy + y²; A (1; 1); (6; 8).

Вариант 26

Задание 1.

Найти производные данных функций.

а)

б)

в)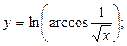

г)

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) б) .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при a=0,53, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=-1/6x³-1/4x²+x-; [-3;2].

Задание 5.

Гипотенуза прямоугольного треугольника равна с . При каком остром угле треугольника его площадь окажется наибольшей и чему она равна?

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .

Задание 7.

Составить уравнение касательной к кривой в точке t=1.

Задание 8.

Найти полную производную сложной функции:

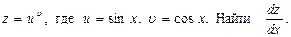
Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = y² + 2x² +3x + 4y – 2; A (3; 4); B (2,98; 3,91).

Задание 10.

Дана функция u = f (x; y; z), точка А (x₀; y₀; z₀) и вектор 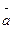(а₁; а₂; a₃). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

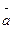u = ln(x²+y²+z²); A (1; 2; 1); =2i+4j+4k.

Вариант 27

Задание 1.

Найти производные данных функций.

а)

б)

в)

г)

д).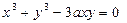

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) б) .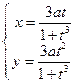

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,39, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=2x³-6x; [-1;2].

Задание 5.

Найти на оси Ох точку, сумма квадратов расстояний которой от точек (2;4) и (8;2) имеет наименьшее значение.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .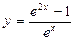

Задание 7.

Показать, что векторы и перпендикулярны.

Задание 8.

Найти полную производную сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 2x² + 2y² + 10x + 8y; A (6; 4); B (6,05; 3,98).

Задание 10.

Дана функция u = f (x; y; z), точка А (x₀; y₀; z₀) и вектор 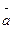(а₁; а₂; a₃). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

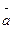u = ; А (x₀; y₀; z₀); a =6i+3j-6k.

Вариант 28

Задание 1.

Найти производные данных функций.

а)

б)

в)

г)

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) б) .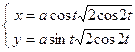

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,81, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=-5x³+6x²+8; [-2;2].

Задание 5.

Найти наибольшую площадь прямоугольника, имеющего периметр 48 см.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .

Задание 7.

Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением 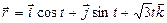в точке t = p/2.

Задание 8.

Найти частные производные сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 2x² + 4xy + 6y² ; A (4; 2); B (3,96; 2,04).

Задание 10.

Дана функция u = f (x; y; z), точки А (x₀; y₀; z₀) и А₁(х₁; y₁; z₁). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .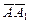

u = ; A (1; 1; 1); А₁ (3; 2; 3).

Вариант 29

Задание 1.

Найти производные данных функций.

а)

б)

в)

г)

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а)б) .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,14, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f(x)=1/6x³-2x; [-3;4].

Задание 5.

К гальваническому источнику тока с электродвижущей силой в 4 в и внутренним сопротивлением 1 ом подключено сопротивление R. При каком значении R можно получить наибольшую мощность во внешней цепи? Определить наибольшую мощность тока во внешней цепи.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б) .

Задание 7.

Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t₀.

Задание 8.

Найти частные производные сложной функции:

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 6x² - 2xy +2x + 2y; A (2; 6); B (2,06; 5,92).

Задание 10.

Дана функция u = f (x; y; z), точки А (x₀; y₀; z₀) и А₁(х₁; y₁; z₁). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .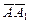

u =xy²z³; A (3; 2; 1); А₁ (5; 4; 2).

Вариант 30

Задание 1.

Найти производные данных функций.

а)

б)

в)

г)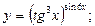

д).

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).