Описание установки и вывод расчетной формулы. В комплект лабораторной установки входят баллистический маятник, пневматическое ружье, пуля, весы, мерная линейка.

В комплект лабораторной установки входят баллистический маятник, пневматическое ружье, пуля, весы, мерная линейка.

Баллистический маятник (рисунок 1) представляет собой тело 2 с массой M, свободно подвешенное на нерастяжимой нити.

Рисунок 1 Схема лабораторной установки

Вылетевшая из воздушного ружья пуля 1, имея скорость ®u, ударяет в центр маятника 2 (центральный удар). Предполагается, что пуля 1 и тело 2 составляют замкнутую систему. Если в результате удара пуля застревает в теле 2 (абсолютно неупругий удар), система начинает двигаться как единое целое с массой M + m со скоростью ®u₂. Для абсолютно неупругого удара справедлив закон сохранения импульса:

m×®u + M×®u₁ = (M + m)×®u₂, (1)

или в скалярной форме

m×u + M×u₁ = (M + m)×u₂,

где m×u + M×u₁ – импульс системы до удара;

(M + m)×u₂ – импульс системы после удара;

Маятника до удара покоился: u₁ =0, тогда m×u=(M + m)×u₂,а так как M>>m, то m×u = M×u₂ ,

отсюда

_. (2)

Таким образом, в результате удара система «M + m» приобретает кинетическую энергию, с учетом (2):

W_кин = = _. (3)

Обладая кинетической энергией (3), маятник (система «M + m») максимально отклоняется от вертикали на угол a, при котором центр масс системы из положения С₁ поднимается на высоту h до остановки (положение С₂), так что вся кинетическая энергия (3) системы переходит в потенциальную энергию, равную

W_пот = (M + m) × g h_.

Из закона сохранения энергии для замкнутой системы следует W_кин = W_пот или _.

Упрощая уравнение, получаем _.

Отсюда скорость пули:

_. (4)

Величины m и M определяются взвешиванием, неопределенным в (4) остается параметр h. Из рисунка 1 следует

h = DC₁ = OC₁ – OD = OC₁ – OC₂×cos a = l ×(1 – cos a),

где OC₁ = OC₂ = l – длина нити. Заменяя 1 – cosa = 2sin^{2 a}/₂, получаем h = l × 2sin^{2 a}/₂ .

На данной установке отклонение маятника мало (угол a меньше 4°¸5°), следовательно sin ^a/₂ » ^a/₂ и

h = 2l × ( ^a/₂ )². (5)

При выполнении опыта измерение угла a невозможно, поэтому выразим его через отклонение b. Как следует из рисунка 1 или . Тогда из (5) следует .

Подставляя последнее выражение в (4), окончательно получаем зависимость для скорости пули

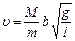_. (6)