Примеры решения задач. Пример 1. Платформа в виде сплошного диска радиусом R=1,5 м и массой m1=180 кг вращается около вертикальной оси с частотой n=10 мин-1

Пример 1. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается около вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость u относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция L_z момента импульса системы платформа-человек остается постоянной:

const, (1)

где J_z - момент инерции платформы с человеком относительно оси z;

w - угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии а в конечном состоянии .

С учетом этого равенство (1) примет вид

(2)

где значения моментов инерции J₁ и J₂ платформы и человека соответственно относятся к начальному состоянию системы; и - к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: . Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном состоянии (в центре платформы)можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека

Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (w = 2pn) и конечной угловой скорости (w^' = u/R, где u - скорость человека относительно пола):

После сокращения на R² и простых преобразований находим скорость

Произведем вычисления:

м/с.

Пример 2. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

где w = 2p/Т. Отсюда амплитуда

(1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -kx, где k - коэффициент квазиупругой силы; х - смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x_max, равном амплитуде:

F_max = kA. (2)

Коэффициент k выразим через период колебаний:

k = mw² = m×4p²/T². (3)

Подставив выражения (1) и (3) и (2) и произведя упрощения, получим

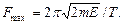
Произведем вычисления:

0,045 м = 45 мм;

Пример 3.Складываются два колебания одинакового направления, выраженные уравнениями

где А₁ = 3 см, А₂ = 2 см, t₁ = 1/6 с, t₂ = 1/3 с, Т = 2 с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме

х = A cos(wt+j), получим

Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

.

Начальные фазы первого и второго колебаний соответственно равны

Произведем вычисления:

с^-1;

Изобразим векторы А₁ и А₂. Для этого отложим отрезки длиной А₁ = 3 см и А₂ = 2 см под углами j₁ = 30^о и j₂ = 60^о к оси 0х. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной геометрической сумме амплитуд А₁ и А₂:А = А₁ + А₂. Согласно теореме косинусов:

Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис. 3):

Произведем вычисления:

см = 4,84 см;

или j = 0,735 рад.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

где А = 4,84 см, w = 3,14 с^-1, j = 0,735 рад.

Таблица вариантов для задания № 2

151. Шарик массой т = 60 г, привязанный к концу нити длиной l₁ =1,2 м, вращается с частотой п₁=2с^-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния l₂ =0,6 м. С какой частотой п₂ будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

152. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой т = 40 кг приложена сила F = 1 кН. Определить угловое ускорение e и частоту вращения п маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

153. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой т = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость w = 9 рад/с.

154. Нить с привязанными к ее концам грузами мас­сами т₁ = 50 г и m₂ = 60 г перекинута через блок диаметром D=4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение e = 1,5 рад/с². Трением и проскальзыванием нити по блоку пренебречь.

155. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению j= At + Bt³, где А = 2 рад/с, В = 0,2 рад/с³. Определить вращающий момент М, действующий на стержень через время t = 2 с после начала вращения, если момент инерции стержня J=0,048 кг× м²

156. По горизонтальной плоскости катится диск со скоростью V = 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s = 18 м.

157. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12c^-l, чтобы он остановился в течение времени Dt = 8 с. Диаметр блока D = 30 см. Массу блока т = 6 кг считать равномерно распределенной по ободу.

158. Блок, имеющий форму диска массой т = 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами т₁ = 0,3 кг и т₂ = 0,7 кг. Определить силы натяжения Т₁ и Т₂ нити по обе стороны блока.

159. К краю стола прикреплен блок. Через блок пе­рекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой - вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а = 5,6 м/с². Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.

160. К концам легкой и нерастяжимой нити, перекинутой через блок, подвешены грузы массами т₁ = 0,2 кг и т₂ = 0,3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0,4 кг, а его ось движется вертикально вверх с ускорением а= 2 м/с²? Силами трения и проскальзывания нити по блоку пренебречь.

161. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой т = 5 кг каждая. Расстояние от каждой гири до оси скамьи l₁ = 70 см. Скамья вращается с частотой п₁ = 1с^-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l₂ = 20 см? Момент инерции человека и скамьи (вместе) относительно оси J = 2,5 кг×м².

162. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью w₁= 4 рад/с. С какой угловой скоростью w₂ будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J =5 кг×м². Длина стержня l=1,8 м, масса m==6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.

163. Платформа в виде диска диаметром D = 3 м и массой m₁=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью w₁ будет вращаться эта платформа, если по ее краю пойдет человек массой m₂ = 70 кг со скоростью V=1,8 м/с относительно платформы?

164. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m₁ = 280 кг, масса человека m₂ = 80 кг.

165. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью w₁=25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью w₂ станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол a=90°? Момент инерции человека и скамьи J равен 2,5 кг×м², момент инерции колеса J₀ = 0,5 кг×м².

166. Однородный стержень длиной l=1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой т=7 г, летящая перпендикулярно стержню и его оси. Определить массу М стерж­ня, если в результате попадания пули он отклонится на угол a=60°. Принять скорость пули V=360 м/с.

167. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n₁=8 мин^--1, стоит человек массой m₁=70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой п₂=10 мин^-1. Определить массу т₂ платформы. Момент инерции человека рассчитывать как для материальной точки.

168. На краю неподвижной скамьи Жуковского диаметром D=0,8 м и массой m₁=6 кг стоит человек массой m₂=60 кг. С какой угловой скоростью w начнет вра­щаться скамья, если человек поймает летящий на него мяч массой m=0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r=0,4 м от оси скамьи. Скорость мяча V=5 м/с.

169. Горизонтальная платформа массой m₁=150 кг вращается вокруг вертикальной оси, проходящейчерезцентр платформы, с частотой n=8 мин^--1. Человек массой т₂= 70 кг стоит при этом на краю платформы. С какой угловой скоростью w начнет вращаться платформа, если человек перейдет от края платформы кеецентру? Считать платформу круглым, однородным диском, а человека — материальной точкой.

170. Однородный стержень длиной l=1,0 м и массой M₁=0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на ²/₃l , абсолютно упруго ударяет пуля массой m = 5 г, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол a=60°. Определить ско­рость пули.

171. На стержне длиной l=30 см укреплены два одинаковых грузика: один — в середине стержня, другой — на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.

172. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A₁ sinw t и y=A₂ cosw t, где A₁=8 см, А₂=4 см, w =2 с^-1. Написать уравнение траектории и построить ее. Показать направление движения точки.

173. Точка совершает простые гармонические колебания, уравнение которых x=Asinwt, где A=5 см, w=2c^-1. В момент времени, когда точка обладала потенциальной энергией П=0,1 мДж, на нее действовала возвращающая сила F=5 мН. Найти этот момент времени t.

174. Определить частоту n простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

175. Определить период Т простых гармонических колебаний диска радиусом R=40 см около горизонтальной оси, проходящей через образующую диска.

176. Определить период Т колебаний математического маятника, если его модуль максимального перемещения Dr = 18 см и максимальная скорость V_max=16 см/с.

177. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x₀ = 4 см, а скорость V₀=10 см/с. Определить амплитуду А и начальную фазу j₀ колебаний, если их период Т=2 с.

178. Складываются два колебания одинакового направления и одинакового периода: х₁=А₁sinw₁t и x₂=A₂sinw₂(t+t), где А₁ = А₂ = 3см, w₁ = w₂ = pc^-1, t=0,5 с. Определить амплитуду А и начальную фазу j₀ результирующего колебания. Написать его уравнение. Построить векторую диаграмму для момента времени t=0.

179. На гладком горизонтальном столе лежит шар массой M=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k=500 Н/м. В шар попадает пуля массой m=10 г, летящая со ско­ростью V=300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период T колебаний шара.

180. Шарик массой m=60 г колеблется с периодом T=2 с. В начальный момент времени смещение шарика x₀=4,0 см и он обладает энергией E=0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.

181. Частица движется со скоростью u = с/3, где с — скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы?

182. Протон с кинетической энергией Т = 3 ГэВ при торможении потерял треть этой энергии. Определить, во сколько раз изменился релятивистский импульс a частицы.

183. При какой скорости b (в долях скорости света) релятивистская масса любой частицы вещества в п = 3 раза больше массы покоя?

184. Определить отношение релятивистского импульса р-электрона с кинетической энергией Т = 1,53 МэВ .к комптоновскому импульсу т_ос электрона.

185. Скорость электрона u = 0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон-вольтах, определить в тех же единицах кинетическую энергию Т электрона.

186. Протон имеет импульс р = 469 МэВ/с*. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое?

187. Во сколько раз релятивистская масса т электрона, обладающего кинетической энергией Т = 1,53 МэВ, больше массы покоя m₀?

188. Какую скорость b (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя?

189. Релятивистский электрон имел импульс p₁ = т_ос. Определить конечный импульс этого электрона (в единицах т_ос), если его энергия увеличилась в п == 2 раза.

190. Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в п = 2 раза.