Основные формулы. Количество вещества тела (системы)

Количество вещества тела (системы)

n = N/N_A,

где N - число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); N_А - постоянная Авогадро

(N_А = 6,02×10²³моль^-1).

Молярная масса вещества

M = m/n,

где m - масса однородного тела (системы); n - количество вещества этого тела.

Относительная молекулярная масса вещества

M_r = Sn_iA_r,i ,

где n_i - число атомов i-го химического элемента, входящих в состав молекулы данного вещества; A_r,i - относительная масса этого элемента. Относительные атомные массы приводятся в таблице Д.И.Менделева.

Связь молекулярной массы М с относительной молекулярной массой вещества

M = M_rk,

где k = 10^-3 кг/моль.

Количество вещества смеси газов

n = n₁ + n₂ + … + n_n = N₁/N_A + N₂/N_A + … + N_n/N_A,

или

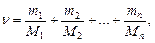
где n_i, N_i, m_i, M_i - соответственно количество вещества, число молекул, масса, молекулярная масса i-го компонента смеси.

Уравнение Менделеева-Клайперона (уравнение состояния идеального газа)

где m - масса газа, М - молекулярная масса газа, R - молекулярная газовая постоянная, n - количество вещества, Т - термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клайперона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T=const, m=const)

pV = const,

или для двух состояний газа

p₁V₁ = p₂V₂;

б) закон Гей-Люссака (изобарный процесс: p=const, m=const)

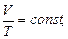
или для двух состояний

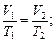
в) закон Шарля (изохорный процесс: V=const, m=const)

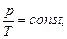
или для двух состояний

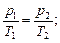
г) объединенный газовый закон (m=const)

или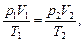

где p₁,V₁,T₁ - давление, объем и температура газа в начальном состоянии; p₂,V₂,T₂ - те же величины в конечном состоянии.

Закон Дальтона, определяющий давление смеси газов,

р = р₁ + р₂ + … + р_n

где p_i - парциальные давления компонентов смеси; n - число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молекулярная масса смеси газов

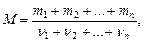
где m_i - масса i-го компонента смеси; ni = m_i/M_i - количество вещества i-го компонента смеси; n - число компонентов смеси.

Массовая доля i-го компонента смеси газа (в долях единицы или процентах)

где m - масса смеси.

Концентрация молекул

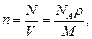
где N - число молекул, содержащихся в данной системе; r - плотность вещества; V - объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов

p = n áe_пñ,

где áe_пñ - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

áe_пñ = kT,

где k - постоянная Больцмана.

Средняя полная кинетическая энергия молекулы

áe_iñ = kT,

где i - число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры

p = nkT.

Скорости молекул:

- средняя квадратичная;

- средняя арифметическая;

- наиболее вероятная,

где m_i - масса одной молекулы.

Относительная скорость молекулы

u = u/u_B,

где u - скорость данной молекулы.

Удельные теплоемкости газа при постоянном объеме (с_v) и постоянном давлении (c_p)

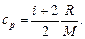
Связь между удельной с и молекулярной С теплоемкостями

с = С/М, С = сМ.

Уравнение Майера

С_p – C_v = R

Внутренняя энергия идеального газа

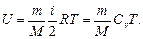
Первое начало термодинамики

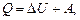
где Q - теплота, сообщенная системе (газу); DU - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил.

Работа расширения газа:

в общем случае;

A = p(V₂-V₁) при изобарном процессе;

при изотермическом процессе;

, или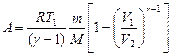

при адиабатном процессе, где g = с_p/c_v - показатель адиабаты.

Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:

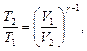
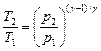
Термический КПД цикла

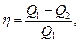
где Q₁ - теплота, полученная рабочим телом от теплоотдатчика; Q₂ - теплота, переданная рабочим телом теплоприемнику.

Термический КПД цикла Карно

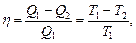
где T₁ и T₂ - термодинамические температуры теплоотдатчика и теплоприемника.

Коэффициент поверхностного натяжения

или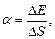

где F - сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; DЕ - изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.

Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости:

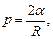
где R - радиус сферической поверхности.

Высота подъема жидкости в капиллярной трубке

где q - краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R - радиус канала трубки; r - плотность жидкости; g - ускорение свободного падения.

Высота подъема жидкости между двумя близкими параллельными друг другу плоскостями

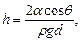
где d - расстояние между плоскостями.