Линеаризация уравнений динамики

Процедуру линеаризации модели динамики рассмотрим на примере дифференциального уравнения второго порядка

или

,

где F – нелинейная дифференцируемая функция своих аргументов.

Уравнение статики можно получено из него, приравнивая нулю производные:

.

Особенностью линеаризации динамики является то, что переменные рассматриваются как независимые аргументы.

Линеаризацию динамики обычно осуществляют относительно некоторого номинального статического режима. Как и ранее переходим к отклонениям:

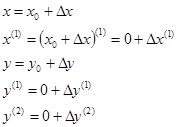
Как видно из формул, номинальные значения скорости, ускорения и т.п. равны нулю (в статическом режиме все производные равны нулю).

Значение y₀ должно быть вычислено из уравнения статики .

Теперь, выражая приращение функции F через приращения всех своих аргументов с учетом формул, получим:

.

Еще раз подчеркнем, что производные под знаком функции F рассматриваются как независимые аргументы.

Уравнение может быть записано в стандартном виде

.

Уравнение называется линеаризованным уравнением динамики в отклонениях.

Оно представляет собой линейное дифференциальное уравнение с постоянными коэффициентами.

В общем случае линеаризованное уравнение для звена с одним входом имеет вид

.

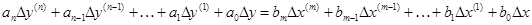Из уравнения динамики можно получить уравнение статики

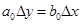или , где .

Коэффициенты линеаризованной модели зависят от номинального режима, а точность от отклонения переменных от номинальных значений.

Таким образом, достоинства и недостатки линеаризованных моделей:

достоинство: получаем простую модель;

недостатки: справедливы при достаточно малых отклонениях, если режим существенно изменяется, то требуется пересчет модели.