
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линеаризация моделей статики.
Рассмотрим модель одномерного звена (рис.1), заданную гладкой дифференцируемой статической характеристикой y=F(x)

Пусть x0 и y0 номинальные значения входного и выходного сигнала. Перейдем от самих сигналов x и y к их отклонениям от номинальных значений ∆x и ∆y, тогда
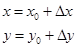
Перенесем начало координат в точку номинального режима, и таким образом перейдем к отклонениям.
Если отклонения достаточно малы, то в окрестности номинального режима (x0,y0) криволинейную характеристику можно заменить отрезком касательной, см. рис.
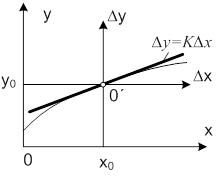
Модель статики в этом случае принимает вид
∆y=K∆x, (1)
где  .
.
Уравнение (1) называется уравнением в отклонениях или линеаризованной моделью звена в статике.
Постоянная K называется коэффициентом усиления или коэффициентом передачи.
Коэффициент усиления численно равен тангенсу угла наклона касательной к статической характеристике в точке номинального режима. В формуле (1) и далее выражение 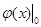 означает, что значение функции
означает, что значение функции  вычисляется в точке
вычисляется в точке  .
.
Если уравнение статики задано аналитически y=F(x), то, переходя к отклонениям и используя формулу приращений, получим  , где
, где 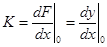 .
.
Аналогичным образом решается задача линеаризации в случае двух входных сигналов u и f
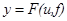
Переходя к отклонениям

и используя формулу приращений получим линеаризованную модель в отклонениях
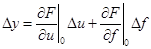 (2)
(2)

K1, K2 – коэффициенты усиления по первому и второму входу соответственно.
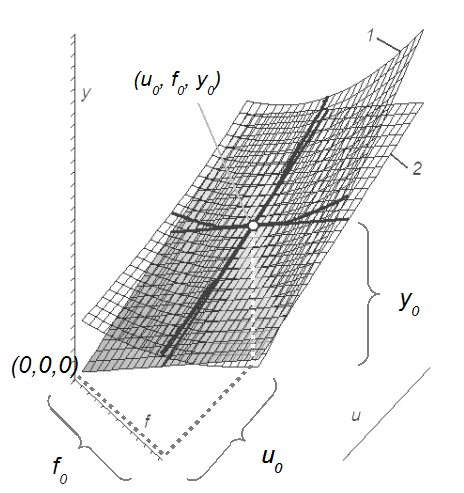
Уравнение (2) – это уравнение касательной плоскости к поверхности заданной уравнением 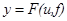 .
.
Дата добавления: 2014-12-30; просмотров: 341; Мы поможем в написании вашей работы!; Нарушение авторских прав |