Понятие об устойчивости. Оценка устойчивости по корням характеристического полинома.

Звено или система называется устойчивой, если переходная составляющая с течением времени стремится к нулю.

Звено или система называется неустойчивой, если переходная составляющая выходного сигнала с ростом времени неограниченно растет.

Звено или система находится на границе устойчивости, если предел переходной составляющей или постоянная, или не существует.

Условия устойчивости/неустойчивости компактно можно записать следующим образом:

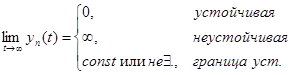
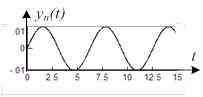
Примеры соответствующих переходных составляющих приведены на рис.

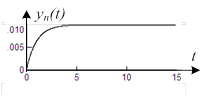
устойчива	на границе устойчивости	неустойчива

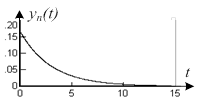
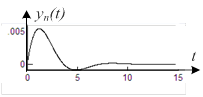
Отметим, что граница устойчивости может быть колебательной и апериодической.

Проведем анализ условий устойчивости.

Рассмотрим переходную составляющую

Она состоит из слагаемых 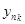. Если все составляющие переходного процесса устойчивы, то процесс устойчив, если хотя бы одна составляющая неустойчива, то процесс неустойчив. Устойчивость отдельной составляющей переходного процесса 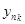зависит от корня D(s), так как

.

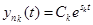Исследуем, как влияет расположение корней D(s) на вид переходного процесса. Будем изображать корни на комплексной плоскости, как показано на рис.

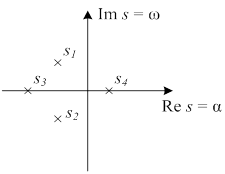
Здесь Re s_i = α_i и Im s_i = ω_i действительная и мнимая части комплексного корня 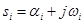, а Re и Im символы вещественной и мнимой части.

Влияние s_i на устойчивость.

1) Пусть корень действительный s_k = α_k ,

тогда переходная составляющая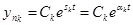

2) Если корни комплексно-сопряженные ,

то сумма переходных составляющих соответствующих этим корням

Из формул видно, что будет с течением времени переходная составляющая стремиться к нулю или расходиться к бесконечности зависит от знака α_k .

Если 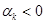, то 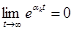(устойчивая)

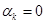, то (на границе устойчивости)

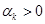, то (не устойчивая)

Примеры:

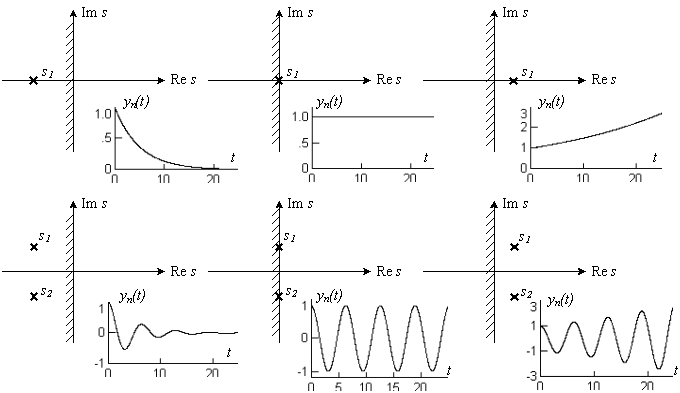
Необходимое и достаточное условие устойчивости:

Для устойчивости звена или системы необходимо и достаточно, чтобы все корни характеристического полинома D(s) имели отрицательные действительные части.

Если хотя бы один корень имеет положительную действительную часть, то звено (или система) не устойчиво.

Если один или два корня имеют действительную часть равную нулю, а остальные отрицательную – система на границе устойчивости.

Условия устойчивости допускают удобную геометрическую интерпретацию

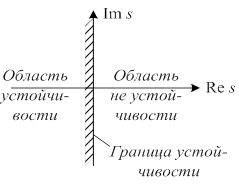
Для устойчивости звена (системы) необходимо и достаточно, чтобы все корни характеристического полинома располагались в левой полуплоскости комплексной плоскости корней.

Мнимая ось, таким образом, является границей устойчивости.

Если хотя бы один корень D(s) располагается в правой полуплоскости, звено (система) – неустойчиво.