
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные формы представления моделей. Линейная модель. Принцип суперпозиции.
Модели статики и динамики могут быть представлены в различной форме.
Модель статики может задаваться
- алгебраическим уравнением (чаще всего)
| Модель | Звено |
| y=2x+3x3 | 
|
| y=2u+uf+0.5f3 | 
|
| в общем случае y = F (x1, x2…..xn), где F – некоторая нелинейная функция или F (y, x1, x2…..xn)=0 – неявная форма | 
|
- Графически
Для звена с одним входом

Для звена с двумя входами строятся семейства статических характеристик

- Таблицей
| x | y |
| x1 | y1 |
| x2 | y2 |
| x3 | y3 |
Динамика системы описывается дифференциальными уравнениями.
Например,
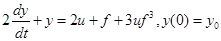 или
или  .
.
В общем случае для звена с одним входом и одним выходом уравнение может быть записано:
 ,
,
где F – некоторая, в общем случае нелинейная функция.
Важно, что модель динамики зависит от производных и входного, и выходного сигнала. Решение ДУ достаточно сложно и в большинстве случаев осуществляется численными методами. Приведенные выше уравнения относятся к классу обыкновенных дифференциальных уравнений. Большинство же объектов нефтепереработки и нефтехимии являются объектами с распределенными параметрами и описываются дифференциальными уравнениями в частных производных, что еще больше усложняет задачу. Поэтому там, где это возможно, стараются заменить их более простыми уравнениями.
Из уравнения динамики легко получить уравнение статики, приравняв все производные нулю.
Так для уравнения рассмотренного выше:
 .
.
Помимо дифференциальных уравнений для описания динамики системы могут использоваться разные частные модели. Например, отклик (реакция) объекта (звена) на специально подобранные входные воздействия и т.д.
Важным классом являются линейные модели. В уравнениях линейных моделей входные и выходные сигналы и их производные входят линейно (могут быть умножены на коэффициент и сложны друг с другом).
Например, модель  линейная,
линейная,
а модель 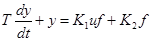 нелинейная, из-за наличия K1uf – нелинейного члена уравнения.
нелинейная, из-за наличия K1uf – нелинейного члена уравнения.
Для линейных систем справедлив принцип суперпозиции (наложения):
Реакция звена (системы) на сумму входных воздействий равна сумме реакций на каждое воздействие в отдельности.
Так, если y1, y2, y3 реакции на входные воздействия x1, x2, x3 соответственно, то реакция сумму воздействий
x=a1x1+a2x2+a3x3
равна
y= a1y1+a2y2+a3y3
Метод наложения широко используется в электротехнике при расчете цепей с несколькими источниками. Линейные модели являются наиболее простыми из всех, легко решаются линейные ДУ, а принцип наложения позволяет независимо исследовать свойства звена, с несколькими входами по каждому входу в отдельности.
Дата добавления: 2014-12-30; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |