
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальное уравнение. Характеристический полином.
Мы переходим к изучению линейных систем АСР, то есть систем, которые описываются линейными моделями. Поскольку все реальные системы нелинейные, то под линейными моделями будем понимать линеаризованные модели реальных нелинейных систем.
Будем рассматривать модели, описываемые линейными дифференциальными уравнениями с постоянными коэффициентами

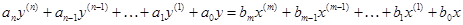 ,
,
где x(t), y(t) – входной и выходной сигналы соответственно,
ai, bi – постоянные коэффициенты.
Для реальных систем справедливо условие физической реализуемости
m≤n,
где n – порядок дифференциального уравнения или, что эквивалентно, порядок звена или системы.
Уравнение может описывать как отдельное звено, так и систему в целом. Для решения ДУ должны быть заданы n начальных условий
 .
.
В частном случае они могут быть нулевыми 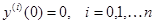 .
.
ДУ может быть записано более компактно
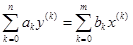
Отметим, что под x и y мы будем понимать отклонения переменных от их номинальных значений ∆x и ∆y, символ ∆ для простоты будем опускать. Поэтому равенство x=0 эквивалентно следующему x=x0, ∆x=0.
Важной характеристикой ДУ является характеристический полином D(s), образуемый из коэффициентов ai
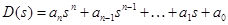 ,
,
где s – в общем случае комплексная переменная.
D(s) получается из левой части ДУ заменой y(i) на si.
Корни характеристического полинома обозначим
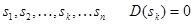
Среди корней могут быть как действительные 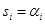 ,так и комплексно-сопряженные
,так и комплексно-сопряженные 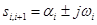 . Здесь
. Здесь 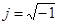 – мнимая единица.
– мнимая единица.
Решение ДУ имеет следующий вид
 ,
,
где yп(t) – переходная составляющая, определенная как общее решение однородного ДУ (уравнение с нулевой правой частью),
yвын(t) – вынужденная составляющая, частное решение неоднородного ДУ,
Ck – постоянные интегрирования, зависящие от начальных условий,
sk – корни характеристического полинома D(s).
Как видно, переходная составляющая существенно зависит от корней D(s) и определяется суммой экспонент действительных и/или комплексных.
Вынужденная составляющая зависит от входного сигнала.
Если звено имеет два входа,
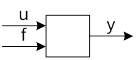
то ДУ может быть записано следующим образом
 .
.
Уравнение статики получается после обнуления производных
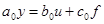 .
.
Дата добавления: 2014-12-30; просмотров: 466; Мы поможем в написании вашей работы!; Нарушение авторских прав |