
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основні фізичні поняття
| № п/п | Автор | Назва, видання |
| Основна | ||
| Г.В. Осовська, О.А. Осовський | Основи менеджменту, - К: Кондор, 2010 | |
| Г.В. Осовська, І.В. Копитов | Основи менеджменту, практикум, - К: Кондор, 2010 | |
| А.В. Шегда | Менеджмент, - К: Знання, 2001 | |
| Ф.І. Хміль | Менеджмент, - К: Вища школа, 2008 | |
| Допоміжна | ||
| Мескон М.Х. та інш | Основи менеджменту – М: 2000 | |
| О.В. Рудінська та інш | Менеджмент, - К: Ніка-Центр, 2002 | |
| О.П. Подсолонко | Менеджмент: теорія і практика, - К: ИЧЛ, 2003 | |
| О.М. Гірняк, П.П. Лазановський | Менеджмент, - Л: Новий світ, 2002 |
Основні фізичні поняття
Явище електромагнетизму було відкрито в 1820 році датським фізиком
Г.Х. Ерстедом, суть якого полягає в тому, що при протіканні по провіднику
електричного струму навколо останнього утворюється магнітне поле.
Був установлений закон електромагнетизму: потокозчеплення електричної котушки прямо пропорційно силі електричного струму й індуктивності котушки.
Математичний запис закону електромагнетизму наступний:
 , ,
| (3.1) |
де y – потокозчеплення котушки, Вб;
w – кількість витків котушки;
Ф – магнітний потік, Вб;
L – індуктивність котушки, Гн;
i – сила електричного струму в котушці, А.
Представимо описане явище схематично (рис.3.1).
 Явище електромагнітної індукції відкрив у
Явище електромагнітної індукції відкрив у
1831 році англійський фізик Майкл Фарадей, суть якого полягає в наступному: якщо провідний контур пронизується змінним магнітним потоком, то в контурі наводиться електрорушійна сила.
Закон електромагнітної індукції: значення
електрорушійної сили, яка наводиться в контурі, прямо пропорційно кількості витків контуру і швидкості зміни
магнітного потоку.
Математичний запис закону:
 , ,
| (3.2) |
де е – електрорушійна сила, В;
w – кількість витків котушки;
Ф – магнітний потік, Вб;
t – поточний час, с.
 . .
|
Приклад 3.1
Котушка зі 100 витків має індуктивність 0,1 Гн;
по котушці протікає струм i = 10 sin wtА.
Визначити магнітний потік усередині котушки.
Рішення.
З (3.1) знаходимо магнітний потік:
 . (3.1а)
. (3.1а)
Підставляємо значення фізичних величин і одержуємо:
 .
.
Фізична суть знака «мінус» полягає в наступному: якщо в даний
момент часу магнітний потік, що пронизує контур, збільшується, то він наводить е.р.с., яка створить електричний струм, а останній свій магнітний потік, який буде спрямований проти основного потоку і навпаки.
 Розглянемо це на графіку (рис.3.2).
Розглянемо це на графіку (рис.3.2).
Явища електромагнетизму й електромагнітної індукції лежать в основі принципу дії генераторів змінного синусоїдного струму.
Приведемо варіант конструктивної схеми генератора змінного синусоїдного струму (рис.3.3).
 Магнітний потік створюється струмом
Магнітний потік створюється струмом
намагнічування I. Провідний контур (рамка) розміщенний на осі між полюсами електромагніта. Якщо рамку привести в обертання, то магнітний потік, що пронизує рамку, буде змінюватися в часі за синусоїдним законом і у рамці буде наводитися е.р.с., яка також буде змінюватися за синусоїдним законом в залежності від кута відхилення рамки від горизонтального положення (рис.3.2, 3.3), тобто
| е = Em ×sina, | (3.3) |
де Еm – амплітудне (максимальне)
значення е.р.с. (при вертикальному
положенні рамки), В;
a – кут відхилення рамки від
горизонтального положення, рад (град);
e – миттєве значення е.р.с.
для заданого кута відхилення рамки, В.
Кут відхилення рамки залежить у часі від кутової швидкості обертання рамки:
| a = w × t, | (3.4) |
де w – кутова швидкість обертання рамки, рад/с (град/с);
t – поточний час, с.
Таким чином, підставивши (3.4) у (3.3), одержимо залежність е.р.с. від кутової швидкості обертання рамки:
| е = Em × sinw t, | (3.5) |
Приклад 3.2
Котушка індуктивності, яка має 100 витків,
пронизується магнітним потоком ф = 0,01 sin wtВб, w = 314 с–1.
Визначити електрорушійну силу, яка наводиться в котушці.
Рішення.
Підставляємо значення фізичних величин у (3.2) і одержуємо:
 .
.
Якщо рамку замкнути за допомогою щіткового механізму на резистор, то
виникає синусоїдний струм:
| i = Im × sinw t, | (3.6) |
де Im – амплітудне (максимальне) значення струму
(при амплітудному значенні е.р.с.), А;
i – миттєве значення струму, А.
Покажемо графік i = f(t) на рис.3.4.
 Запишемо кутову швидкість обертання рамки через частоту (кількість оборотів за
Запишемо кутову швидкість обертання рамки через частоту (кількість оборотів за
секунду):
| w = 2p×f, | (3.7) |
де f – частота обертання рамки, (1/с) Гц.
З такою же частотоюf буде змінюватися й електричний струм.
Час одного обороту рамки позначимо через Т; таким же буде і час одного
повного коливання струму, назвемо його періодом струму.
У Європі частота струму дорівнює 50 Гц, тобто f = 50 Гц (1/с).
Тоді період струму Т = 0,02 с, тобто
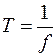 . .
| (3.8) |
У загальному випадку в момент часу t = 0 рамка може знаходитися під певним кутом відносно горизонтального положення і тоді миттєве значення струму
записується в такий спосіб:
| i = Im×sin(w t + yi), | (3.9) |
де yi – початкова фаза струму (початковий кут відхилення рамки), рад (град);
(w t+ yi) – поточна фаза струму, рад (град).
 Синусоїдні величини (струми, напруги, е.р.с., потенціали) зображують на
Синусоїдні величини (струми, напруги, е.р.с., потенціали) зображують на
площині за допомогою векторів. Для цього береться амплітудне значення синусоїдної величини та в обраному масштабі відкладається у видгляді відрізка прямої під
кутом до осі відліку, який дорівнює початковій фазі зображуваної величини. Якщо початкова фаза позитивна, то кут відліку відкладається проти годинникової стрілки, якщо негативна – за годинниковою стрілкою. Як приклад струм i = Im × sin(w t+ 45°)А
зображений на рис.3.5.
Кутову швидкість обертання рамки називають круговою (кутовою) частотою струму:
w =2p×f =2p×50= 314 рад/с
і графік i = f ( t ) найчастіше будують у видгляді i = f¢ ( wt ), тобто миттєве значення струму у функції миттєвого значення фази струму (миттєвого кута повороту
рамки).
У видгляді вектора струм зображують для моменту часу t = 0. Миттєве
значення струму в будь-який інший момент часу (іншої фази струму) є проекція
вектора на вертикальну ось (рис.3.5).
Приклад 3.3
По котушці протікає струм i = 15 sin (wt +30°) А.
Зобразити струм у видгляді вектора.
 Рішення.
Рішення.
Вибираємо масштаб струму mi = 0,5 А/мм і
будуємо вектор струму (рис.3.6).
Опір провідника змінному струму (активний) залежить від частоти струму і пов'язаний з тим, що в результаті витиснення струму на поверхню провідника переріз провідника як би зменшується, що приводить до збільшення його опору в порівнянні з постійним струмом. Витиснення струму на поверхню провідника (поверхневий ефект) виникає внаслідок явища електромагнітної індукції. Змінне магнітне поле навколо провідника, створене змінним струмом у провіднику, наводить е.р.с. самоіндукції. Якщо представити провідник у вигляді безлічі паралельних ниток, по яких проходять свої струми, то найбільша кількість магнітних силових ліній зчеплено з центральними нитками і там наводиться найбільша е.р.с., яка перешкоджає струму і витісняє його на поверхню (рис.3.7).
 |
 Зображується активний опір на розрахункових схемах у такий спосіб: .
Зображується активний опір на розрахункових схемах у такий спосіб: .
З курсу фізики відомо, що індуктивність котушки (провідника) залежить від квадрата кількості витків, магнітної проникності середовища, по якому замикається магнітний потік, площі внутрішнього перерізу котушки і довжини
середньої силової лінії магнітного потоку, тобто
 , ,
| (3.10) |
де w – кількість витків котушки;
m – відносна магнітна проникність середовища,
по якому замикається магнітний потік;
m0 – магнітна постійна (m0 = 4p×10–7 Гн/м), Гн/м;
S – площа внутрішнього перерізу котушки, м2;
l – довжина середньої магнітної силової лінії, м.
 . .
|
 Індуктивність на розрахункових схемах зображується в такий спосіб:
Індуктивність на розрахункових схемах зображується в такий спосіб:
.
Приклад 3.4
Котушка індуктивності без феромагнітного осердя має 1000 витків.
Площа внутрішнього перерізу котушки дорівнює 400 см2,
довжина середньої силової лінії магнітного потоку котушки дорівнює 12,56 см.
Визначити індуктивність котушки.
Рішення.
Підставляємо значення параметрів котушки в (3.10) і одержуємо:
 .
.
Діюче значення змінного синусоїдного струму. Змінний синусоїдний струм, проходячи по провіднику, супроводжується тепловою дією незалежно від
напряму струму. Миттєва потужність, яка виділяється в провіднику
| р = r×i2, | (3.11) |
де r – активний опір, Ом;
i – миттєвий струм, А;
р – миттєва потужність, Вт.
Знайдемо кількість тепла (енергії), що виділиться в провіднику за період струму:
 . .
| (3.12) |
Замінимо дійсний змінний синусоїдний струм еквівалентним постійним струмом, при якому за період виділиться така ж кількість тепла в тому же провіднику:
| W = r×I2×T, | (3.13) |
де I – еквівалентний постійний струм, А.
Дорівнявши (3.12) до (3.13), знаходимо:
 . .
| (3.14) |
Величину еквівалентного постійного струму назвали діючим значенням змінного синусоїдного струму. За аналогією введемо поняття діючих значень е.р.с. і
напруги:
 ; ;
| (3.15) |
 . .
| (3.16) |
Електровимірювальні прилади показують діючі значення вимірюваних величин (струму, напруги).
Приклад 3.5
У колі протікає електричний струм i = 14,1 sin (wt –37°) А.
Визначити показання амперметра, включеного в коло.
Рішення.
Амперметр показує діюче значення струму, яке визначаємо за (3.14), підставивши амплітуду струму:
 .
.
Запитання для самоконтролю
1. У чому суть явища електромагнетизму?
2. Сформулюйте закон електромагнетизму.
3. Математично запишіть і розшифруйте закон електромагнетизму.
4. У чому суть явища електромагнітної індукції?
5. Сформулюйте закон електромагнітної індукції.
6. Математично запишіть і розшифруйте закон електромагнітної індукції.
7. Поясніть фізичну суть знака «мінус».
8. Приведіть приклад використання явища електромагнітної індукції в техніці.
9. Складіть і опишіть конструктивну схему машинного генератора
змінного синусоїдного струму.
10. Опишіть принцип дії машинного генератора змінного синусоїдного струму.
11. Поясніть, чому в генераторі наводиться синусоїдна е.р.с.,
запишіть і розшифруйте її математичний вираз.
12. Запишіть і розшифруйте математичний вираз
миттєвої напруги на затисках ідеального генератора.
13. Як одержати синусоїдний струм?
14. Запишіть і розшифруйте математичний вираз миттєвого синусоїдного струму.
15. Що таке амплітуда струму?
16. Що таке частота струму?
17. Що таке період струму?
18. Що таке кругова частота струму?
19. Що таке початкова фаза струму?
20. Що таке миттєва фаза струму?
21. Як зобразити струм за допомогою радіус-вектора?
22. Поясніть фізичну суть активного опору провідника змінному струму
в порівнянні з опором провідника постійному струму.
23. Що таке індуктивність котушки? Від чого вона залежить?
24. Що розуміється під діючим значенням змінного синусоїдного струму?
Як його розрахувати через амплітудне значення струму?
25. Як розрахувати діюче значення е.р.с. через амплітудне значення?
26. Як розрахувати діюче значення напруги через амплітудне значення?
Завдання для самоконтролю
У колі протікає струм i = 28,2sin (wt – 30°) А.
1. Зобразіть цей струм графічно у видгляді i = f (wt).
Укажіть на графіку період і амплітуду струму.
2. Зобразіть цей струм за допомогою радіус-вектора.
3. Знайдіть показання амперметра, по якому протікає зазначений струм.
Дата добавления: 2015-01-01; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |