
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пространственная инверсия Р. Чётность
Операция пространственной инверсии P заключается в преобразовании:
x, y, z,  ,
, 
 -x, -y, -z, -
-x, -y, -z, -  ,
,  .
.
Операция P изменяет знак любого полярного вектора:

 -
-  ,
,

 -
-  .
.
Аксиальные векторы при пространственной инверсии не изменяются:


 .
.
Операция пространственной инверсии переводит систему в зеркально симметричную. Зеркальная симметрия наблюдается в процессах под действием сильного и эектромагнитного взаимодействий. Зеркальная симметрия в этих процессах означает, что в зеркально симметричных состояниях переходы реализуются с одинаковой вероятностью. Это означает симметричность распадов относительно плоскости перпендикулярной спину, т.е. угловые распределения распадов поляризованных ядер симметричны под углами θ и π − θ) относительно спина ядра.
Зеркальная симметрия гамильтониана взаимодействия не исключает процессы, в которых зеркальная симметрия нарушена. Примером могут служить некоторые молекулы, которые вращают плоскость поляризации света в противоположные стороны. Это так называемое спонтанное нарушение симметрии. Симметрия гамильтониана относительно зеркального отражения проявляется в том, что наряду с левополяризующими молекулами существуют и правополяризующие молекулы, являющиеся зеркальным отражением друг друга. Нарушение зеркальной симметрии связано с вырождением основного состояния и распространением света в среде, состоящей только из правополяризованных или левополяризованных молекул.
Инвариантность гамильтониана схемы  относительно пространственно-го отражения – инверсии (замены
относительно пространственно-го отражения – инверсии (замены  → -
→ -  ) приводит к закону сохранения четности и квантовому числу чётность.
) приводит к закону сохранения четности и квантовому числу чётность.
Все свойства системы частиц определяются видом гамильтониана  и волновой функции ψ(
и волновой функции ψ(  ), которая является решением соответствующего уравнения Шредингера. В приведенных ниже соотношениях (1)–(23)
), которая является решением соответствующего уравнения Шредингера. В приведенных ниже соотношениях (1)–(23)  обозначает совокупность координат всех А частиц, входящих в состав системы, т.е.
обозначает совокупность координат всех А частиц, входящих в состав системы, т.е.
 ≡
≡  1,
1,  2, ...,
2, ...,  A.
A.
Инвариантность системы к пространственной инверсии означает, что выполняется соотношение для плотности вероятности найти систему в определенной точке многомерного пространства:
|ψ(  )|2 = |ψ(- )|2 = |ψ(-  )|2. )|2.
| (1) |
В результате возникают два возможных преобразования волновой функции в результате пространственной инверсии:
ψ(-  ) = ψ( ) = ψ(  ), ψ(- ), ψ(-  ) = -ψ( ) = -ψ(  ). ).
| (2) |
В первом случае волновая функция системы четная, во втором – нечётная. Соотношения (17.2) можно записать в виде одного равенства
ψ(-  ) = pψ(
) = pψ(  ),
),
где р= ±1 − квантовое число чётность.
Квантовое число четность является собственным значением оператора пространственной инверсии. Определим оператор пространственной инверсии  (оператор чётности) для системы частиц следующим образом:
(оператор чётности) для системы частиц следующим образом:
 ψ( ψ(  ) = ψ(- ) = ψ(-  ). ).
| (3) |
Если подействовать на левую и правую части соотношения (3) ещё раз оператором 
 2ψ( 2ψ(  ) = ) =  ψ(- ψ(-  ) = ψ(- ) = ψ(-  ), ),
| (4) |
получится исходное состояние системы, т.е.  2 − оператор тождественного преобразования.
2 − оператор тождественного преобразования.
Оператор  , волновая функция ψ(
, волновая функция ψ(  ) и квантовое число четности р в силу инвариантности системы относительно пространственного отражения должны быть связаны уравнением на собственные значения
) и квантовое число четности р в силу инвариантности системы относительно пространственного отражения должны быть связаны уравнением на собственные значения
 ψ( ψ(  ) = pψ( ) = pψ(  ). ).
| (5) |
Из (4) и (5) следует, что:
 2ψ(
2ψ(  ) = p2ψ(
) = p2ψ(  ) = ψ(
) = ψ(  ),
),
т.е. p2 = 1 и собственные значения оператора четности  p = ±1.
p = ±1.
В результате получаем

| (6) |
или
ψ(-  ) = ψ(
) = ψ(  ) − чётные функции (состояния),
) − чётные функции (состояния),
ψ(-  ) = -ψ(
) = -ψ(  ) -нечётные функции (состояния).
) -нечётные функции (состояния).
В рассмотренном случае волновая функция ψ(  ) была волновой функцией системы точечных (бесструктурных) частиц. В общем случае волновая функция отдельной частицы имеет вид:
) была волновой функцией системы точечных (бесструктурных) частиц. В общем случае волновая функция отдельной частицы имеет вид:
Ψ =  ψ( ψ(  ), ),
| (7) |
где  описывает внутреннее состояние частицы, а ψ(
описывает внутреннее состояние частицы, а ψ(  ) - перемещение частицы в пространстве как целого. Представление волновой функции Ψ в форме (7) следует из того, что гамильтониан частицы можно представить как сумму гамильтонианов:
) - перемещение частицы в пространстве как целого. Представление волновой функции Ψ в форме (7) следует из того, что гамильтониан частицы можно представить как сумму гамильтонианов:
 ψ +
ψ + 
 ,
,
где  ψ описывает бесструктурную частицу,
ψ описывает бесструктурную частицу,
а 
 -внутреннюю структуру частицы.
-внутреннюю структуру частицы.
Оператор чётности  действует на каждый множитель волновой функции Ψ =
действует на каждый множитель волновой функции Ψ =  ψ(
ψ(  ):
):
 Ψ = Ψ =   · ·  ψ( ψ(  ). ).
| (8) |
Если 
 - инвариантен относительно операции инверсии в пространстве внутренних координат
- инвариантен относительно операции инверсии в пространстве внутренних координат  , то
, то
  ( (  ) = π( ) = π(  ), ),
| (9) |
где π −внутренняя чётность частицы.
Волновая функция ψ(  ) орбитального движения частицы в центральном поле, т.е. движения с определённым орбитальным моментом l, может быть представлена в сферических координатах в виде разложения по сферическим координатам
) орбитального движения частицы в центральном поле, т.е. движения с определённым орбитальным моментом l, может быть представлена в сферических координатах в виде разложения по сферическим координатам
ψ(  ) = Rnl(r)·Ylm(θ,φ). ) = Rnl(r)·Ylm(θ,φ).
| (10) |
Инверсия  → -
→ -  соответствует в сферических координатах преобразованию
соответствует в сферических координатах преобразованию
r → r, θ → π − θ (полярный угол),
φ →π + φ (азимутальный угол),
при котором радиальная часть волновой функции Rnl(r) не изменяется, а Ylm(θ,φ) – собственная функция оператора орбитального момента количества движения (сферическая функция) – преобразуется следующим образом:
| Ylm(π-θ,φ+π) = (-1)lYlm(θ,φ). | (11) |
В результате получим:
 Ψ = π(-1)lΨ Ψ = π(-1)lΨ
| (12) |
Величина (-1)l называется орбитальной чётностью.
Волновую функцию системы Анезависимых частиц можно представить в виде произведения волновых функций отдельных частиц (в более общем случае, в виде линейной комбинации этих произведений):
| ψ(1,2,...,A) = Ψ1·Ψ2·...ΨA, | (13) |
где Ψ1 =  1ψ(
1ψ(  1), Ψ2 =
1), Ψ2 =  2ψ(
2ψ(  2), …, ΨA =
2), …, ΨA =  Aψ(
Aψ(  A).
A).
Таким образом, при движении частиц в центральном поле,
 ψ(1,2,...,A) = π1π2...πA
ψ(1,2,...,A) = π1π2...πA 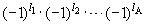 ψ(1,2,...,A),
ψ(1,2,...,A),
полная чётностьсистемы определяется четностью каждой частиц πi и ее орбитальным моментом l.

| (14) |
Для двух частиц:

| (15) |
где L = l1 + l2 – орбитальный момент относительного движения частиц в системе их центра инерции.
Формулы (14), (15) можно применять к реакциям с частицами, когда частицы до и после столкновения можно считать невзаимодействующими, а также к ядру как системе нуклонов, рассматривая их как независимые частицы, находящиеся в общем ядерном потенциале.
Ядерный гамильтониан

| (16) |
где

V(|  α -
α -  β|) – потенциал взаимодействия нуклонов a и b обладает инвариантностью к пространственной инверсии.
β|) – потенциал взаимодействия нуклонов a и b обладает инвариантностью к пространственной инверсии.
Инвариантность гамильтониана относительно пространственной инверсии (16) означает, что атомное ядро не изменяет своих свойств при  → -
→ -  и ядерные состояния можно характеризовать определенной четностью, которая в ядерных взаимодействиях сохраняется.
и ядерные состояния можно характеризовать определенной четностью, которая в ядерных взаимодействиях сохраняется.
Электромагнитные процессы также инвариантны относительно пространственной инверсии, и четность в них сохраняется. Это следует из того, что уравнения Максвелла не изменяются при преобразовании  → -
→ -  . В отличие от сильных и электромагнитных взаимодействий гамильтониан слабого взаимодействия не обладает инвариантностью относительно зеркального преобразования
. В отличие от сильных и электромагнитных взаимодействий гамильтониан слабого взаимодействия не обладает инвариантностью относительно зеркального преобразования  → -
→ -  . Это означает, что в слабых взаимодействиях четность не сохраняется. Системы, в которых слабые силы играют большую роль, нельзя характеризовать определенной четностью.
. Это означает, что в слабых взаимодействиях четность не сохраняется. Системы, в которых слабые силы играют большую роль, нельзя характеризовать определенной четностью.
Смысл имеют лишь относительные внутренние чётности. Для протона, состоящего из трех кварков с положительной внутренней четностью и нулевыми относительными орбитальными моментами, естественно получаем внутреннюю чётность π(p) = +1. Нейтроны также имеют внутреннюю чётность π(n) = +1. Внутренние чётности частиц определяют, исходя из их кваркового состава и орбитального момента l кварков в составе адрона.
Соотношение  ψ(
ψ(  ) = ψ(-
) = ψ(-  ) справедливо для скалярных функций ψ(
) справедливо для скалярных функций ψ(  ). При действии оператора
). При действии оператора  на векторную функцию
на векторную функцию  (
(  ) следует изменить не только знаки радиусов-векторов частиц (
) следует изменить не только знаки радиусов-векторов частиц (  → -
→ -  ), но также и знаки всех трёх компонент вектора
), но также и знаки всех трёх компонент вектора  (Ax → -Ax, Ay → -Ay, Az → -Az), что происходит при изменении направления всех координатных осей на противоположные.
(Ax → -Ax, Ay → -Ay, Az → -Az), что происходит при изменении направления всех координатных осей на противоположные.
Поэтому для любого истинного (полярного) вектора имеет место соотношение 
 (
(  ) = -
) = -  (-
(-  ).
).
Для фотона внутренняя четность отрицательна π(γ) = -1. Это является следствием того, что электромагнитное поле векторное. Оно описывается векторным потенциалом  , который эквивалентен волновой функции фотона, а для векторной функции
, который эквивалентен волновой функции фотона, а для векторной функции
  ( (  ) = - ) = -  (- (-  ), ),
| (17) |
что позволяет приписать фотону π(γ) = -1.
Внутренние чётности частиц и античастиц с полуцелым спином (фермионов) противоположны, с целым спином (бозонов) – одинаковы.
Внутренние чётности частиц определяют из распадов и реакций с участием частиц с известной внутренней чётностью на основе закона сохранения полной чётности.
В. Вайспопф, Л. Родберг: «Новые недавно выполненные в ядерной физике опыты свидетельствуют о том, что некоторые основные свойства природы имеют далеко не тот характер, который им приписывали. В истории физики редко случалось, чтобы изменение основных принципов следовало из результатов всего лишь нескольких опытов.
Прежде чем обсудить сами опыты, нужно рассмотреть основной закон, на который посягают полученные результаты. Это закон четности. Он может быть выражен в следующей форме: каждый процесс, происходящий в природе, может протекать и так, каким он виден отраженным в зеркале. Это значит, что природа зеркально симметрична. Зеркальное изображение любого объекта есть также возможный объект природы; движение любого объекта, рассматриваемого в зеркале, есть также движение, разрешаемое законами природы. Любой выполненный в лаборатории опыт может быть выполнен таким образом, каким он кажется в зеркале, и любой полученный при этом эффект должен быть зеркальным изображением действительного эффекта. Выражаясь кратко, законы природы инвариантны относительно отражения.
Опыт был выполнен Ли в Государственном Бюро стандартов в Вашингтоне, где имеется криогенная техника для опытов при очень низких температурах. Опыт осуществили By из Колумбийского университета и Амблер, Хейворд, Хоппс и Хадеон из Государственного Бюро стандартов. Они ориентировали вращение ядер кобальта и сравнили электронные интенсивности в двух противоположных относительно оси вращения направлениях.
Этот опыт имеет несколько замечательных особенностей. Он принадлежит к тем опытам, произвести которые отважились бы немногие физики, ибо его результат «с очевидностью» следовал из зеркальной симметрии. Большие открытия всегда связаны с тем, что «очевидное» подвергается сомнению. В этом случае заслуга принадлежит двум физикам теоретикам – Ли из Колумбийского университета и Янгу из Института проблемных исследований, которые указали экспериментаторам на необходимость этого опыта. Ли и Янг предположили, что для некоторых слабых взаимодействий, подобных β-распаду, принцип четности может оказаться неверным»
Дата добавления: 2015-01-01; просмотров: 866; Мы поможем в написании вашей работы!; Нарушение авторских прав |