
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зарядовая чётность
Операция  зарядового сопряжения − это операция замены знаков всех зарядов на противоположные:
зарядового сопряжения − это операция замены знаков всех зарядов на противоположные:
x, y, z,  , ,  , Q, B, Le, Lμ, Lτ, s, c, b, t , Q, B, Le, Lμ, Lτ, s, c, b, t
| 
| x, y, z,  , ,  , -Q, -B, -Le, -Lμ, -Lτ, -s, -c, -b, -t , -Q, -B, -Le, -Lμ, -Lτ, -s, -c, -b, -t
|
При этом пространственные координаты x, y, z,, импульс  и спин
и спин  частицы не изменяются. Так, например, в случае барионов и лептонов изменение знака электрического заряда сопровождается изменением знаков барионного B и лептонных Le, Lμ и Lτ зарядов и, как следствие, изменением знака магнитного момента
частицы не изменяются. Так, например, в случае барионов и лептонов изменение знака электрического заряда сопровождается изменением знаков барионного B и лептонных Le, Lμ и Lτ зарядов и, как следствие, изменением знака магнитного момента  . Абсолютная величина магнитного момента не изменяется.
. Абсолютная величина магнитного момента не изменяется.
| Электрический заряд Q | 
|
| Барионный заряд B | 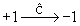
|
| Лептонные заряды Le, Lμ, Lτ | 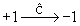
|
| Спин J | 
|
| Магнитный момент | 
|
| Квантовые числа s, c, b, t |  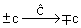  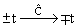
|
Знаком перед магнитным моментом обозначен магнитный момент параллельный и антипараллельный вектору спина, т.е. спиральность частицы.
Операция зарядового сопряжения переводит частицу в античастицу и наоборот.
 |частица> = |античастица>, |частица> = |античастица>,  |античастица> = |частица> |античастица> = |частица>
| (18) |
Это утверждение несправедливо для нейтрино − частиц, имеющих определённое значение спиральности. Если операцию зарядового сопряжения применить дважды, то получится частица с исходными квантовыми числами:
 2|частица> = 2|частица> =  |античастица> = |частица>. |античастица> = |частица>.
| (19) |
Оператор  2 - это оператор тождественного преобразования, имеющий собственные значения c = ±1. Действительно, уравнение на собственные значения имеет вид:
2 - это оператор тождественного преобразования, имеющий собственные значения c = ±1. Действительно, уравнение на собственные значения имеет вид:
 |частица> = c|частица>. |частица> = c|частица>.
| (20) |
Отсюда, рассматривая совместно (19) и (20), получаем c = 1 и c = ±1. Однако оператор  далеко не всегда имеет собственные значения, т. е. не для всех частиц или систем частиц формально записанное соотношение (20) имеет физический смысл. Если подействовать оператором зарядового сопряжения
далеко не всегда имеет собственные значения, т. е. не для всех частиц или систем частиц формально записанное соотношение (20) имеет физический смысл. Если подействовать оператором зарядового сопряжения  на состояние |π+>, описывающее π+-мезон:
на состояние |π+>, описывающее π+-мезон:
 |π+> = |π->. |π+> = |π->.
| (21) |
Получаем состояние |π->, отличное от исходного состояния |π+>. Поэтому для π±-мезона невозможно выполнение уравнения (20). Это свойство оператора  обусловлено тем, что он не коммутирует с оператором заряда.
обусловлено тем, что он не коммутирует с оператором заряда.
Оператор зарядового сопряжения имеет собственные значения только для полностью нейтральных (истинно нейтральных) частиц, таких как фотон γ, нейтральные мезоны qiqi − π0, η,η', ρ,  , ω и другие, а также для полностью нейтральных систем частиц π+π-, e+e- и др. Для таких частиц (систем) соотношение (20) приобретает смысл и величина C, называемая зарядовой чётностью, равна либо +1, либо -1. Зарядовая чётность с является мультипликативным квантовым числом.
, ω и другие, а также для полностью нейтральных систем частиц π+π-, e+e- и др. Для таких частиц (систем) соотношение (20) приобретает смысл и величина C, называемая зарядовой чётностью, равна либо +1, либо -1. Зарядовая чётность с является мультипликативным квантовым числом.
Как приписать определённое значение зарядовой чётности истинно нейтральным частицам? Квант электромагнитного поля – фотон – описывается векторным потенциалом  (
(  ,t), который создается электрическими зарядами. При зарядовом сопряжении все заряды изменяют знаки, а значит, изменяет знак и создаваемый ими векторный потенциал
,t), который создается электрическими зарядами. При зарядовом сопряжении все заряды изменяют знаки, а значит, изменяет знак и создаваемый ими векторный потенциал  . Поэтому, обозначая состояние фотона |γ> = |
. Поэтому, обозначая состояние фотона |γ> = |  >, можно записать
>, можно записать
 | |  > = -| > = -|  >. >.
| (22) |
Таким образом, зарядовая чётность фотона отрицательная
C(γ) = -1.
Используя то обстоятельство, что электромагнитное взаимодействие С-инвариантно и зарядовая чётность в этом взаимодействии сохраняется, можно приписать определённую зарядовую чётность π0-мезону. Так как π0 распадается в результате электромагнитного взаимодействия на два фотона: π0→2γ, то он должен иметь положительную зарядовую чётность:
 |π0> = |π0> =  |γ>· |γ>·  |γ> = (-|γ>)·(-|γ>) = +|π0>. |γ> = (-|γ>)·(-|γ>) = +|π0>.
| (23) |
Таким образом, зарядовая чётность π0 положительна
C(π0) = +1.
Сохранение зарядовой чётности запрещает некоторые распады. Так, например, распад π0→3γ за счёт электромагнитного взаимодействия невозможен, т.к. зарядовая чётность π0-мезона +1, в то время как зарядовая чётность трёх γ-квантов (-1)(-1)(-1) = -1.
Получим общее выражение для зарядовой чётности системы фермион-антифермион (позитроний e+e- или q 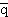 ). Для определённости рассмотрим систему кварк-антикварк с противоположно направленными спинами, т. е. состояние
). Для определённости рассмотрим систему кварк-антикварк с противоположно направленными спинами, т. е. состояние  . Операция зарядового сопряжения изменяет природу обеих частиц, сохраняя их спиновые состояния:
. Операция зарядового сопряжения изменяет природу обеих частиц, сохраняя их спиновые состояния: 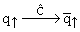 ,
, 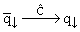 . В результате получается состояние
. В результате получается состояние  , которое возникло бы при перестановке кварка и антикварка с одновременным обменом их спинами. Система q
, которое возникло бы при перестановке кварка и антикварка с одновременным обменом их спинами. Система q 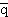 является собственным состоянием оператора
является собственным состоянием оператора  . Поэтому можно записать:
. Поэтому можно записать:
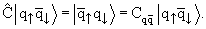
| (24) |
Для того, чтобы вернуться из состояния  в исходное состояние
в исходное состояние  , нужно осуществить замену q↔
, нужно осуществить замену q↔ 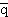 и вновь поменять спиновые состояния кварков, т.е. одновременно переставить частицы и их спины. Операция перестановки qи
и вновь поменять спиновые состояния кварков, т.е. одновременно переставить частицы и их спины. Операция перестановки qи 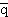 в системе их центра масс эквивалентна операции пространственной инверсии, т.е. приводит к появлению перед волновой функцией системы множителя полной чётности системы Р. В данном случае P = Pq
в системе их центра масс эквивалентна операции пространственной инверсии, т.е. приводит к появлению перед волновой функцией системы множителя полной чётности системы Р. В данном случае P = Pq  (-1)L = (+1)(-1)(-1)L = -(-1)L = (-1)L+1, где Pq и
(-1)L = (+1)(-1)(-1)L = -(-1)L = (-1)L+1, где Pq и  - внутренние чётности кварка и антикварка (соответственно +1 и -1), а L - их относительный орбитальный момент.
- внутренние чётности кварка и антикварка (соответственно +1 и -1), а L - их относительный орбитальный момент.
Что касается перестановки спинов кварков, то, если спины кварков параллельны (S = 1), то спиновая функция системы симметрична, т.е. не изменяет знак при перестановке спинов. Если спины кварков антипараллельны (S = 0), то спиновая функция антисимметрична, т.е. изменяет знак при перестановке спинов. Обе эти ситуации учитываются введением множителя (-1)S+1 перед волновой функцией системы при перестановке спинов кварков.
Таким образом, зарядовая чётность системы кварк - антикварк  (и любой другой системы фермион-антифермион) является произведением множителя полной чётности системы (-1)L+1 и множителя (-1)S+1, учитывающего характер симметрии спиновой волновой функции системы:
(и любой другой системы фермион-антифермион) является произведением множителя полной чётности системы (-1)L+1 и множителя (-1)S+1, учитывающего характер симметрии спиновой волновой функции системы:

| (25) |
Из закона сохранения зарядовой четности следует, какое число фотонов образуется при распаде парапозитрония и ортопозитрония.
Распад позитрония происходит в результате аннигиляции входящих в его состав e+ и e-, т.е. за счет сохраняющего зарядовую чётность процесса e+ + e- → фотоны, обусловленного электромагнитным взаимодействием. У парапозитрония L = S = 0, а у ортопозитрония L = 0, S = 1. Поэтому зарядовая чётность парапозитрония Cпара = (-1)L+S = (-1)0 = +1, а ортопозитрония − Cорто = (-1)L+S = (-1)1 = -1. Поскольку зарядовая чётность фотона Cγ = -1, то парапозитроний может распадаться только на чётное число фотонов, а ортопозитроний − на нечётное число фотонов. Наиболее вероятен распад с минимально возможным числом фотонов. Распад с одним фотоном в конечном состоянии запрещён законами сохранения энергии и импульса. Поэтому парапозитроний преимущественно распадается на 2 фотона, а ортопозитроний -на 3 фотона.
Кварк-антикварковая (qi 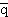 j) структура мезонов делает возможным существование истинно нейтральных мезонов. Все аддитивные квантовые числа (электрический и барионный заряды, кварковый аромат) в мезоне, состоящем из кварка и антикварка одного типа, в сумме равны нулю.
j) структура мезонов делает возможным существование истинно нейтральных мезонов. Все аддитивные квантовые числа (электрический и барионный заряды, кварковый аромат) в мезоне, состоящем из кварка и антикварка одного типа, в сумме равны нулю.

| JPC = | 0-+ | 1-- | 0++ | 1++ | 2++ |
| L = | |||||
| S = |
Рис. 2 - Связанные состояния c 

| JPC = | 0-+ | 1-- | 1+- | 0++ | 1++ | 2++ |
| L = | ||||||
| S = |
Рис. 3 - Связанные состояния b  .
.
На рис. 2 и 3 показаны связанные состояния чармония (c  ) и боттомония (b
) и боттомония (b  ). Приведены спины
). Приведены спины  , четности P, зарядовые четности C, орбитальный L и спиновый S моменты системы кварк-антикварк.
, четности P, зарядовые четности C, орбитальный L и спиновый S моменты системы кварк-антикварк.
 =
=  +
+  .
.
Зарядовая чётность С
Зарядовая чётность сохраняется в сильных и электромагнитных взаимодействиях и не сохраняется в слабых взаимодействиях.
Дата добавления: 2015-01-01; просмотров: 627; Мы поможем в написании вашей работы!; Нарушение авторских прав |