Розв'язок

Рівняння власних коливань має вигляд:

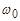x = А₀ sin t,

Зсув по фазі між власними та вимушеними коливаннями за умо­вою дорівнює - 3 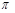/4, отже

tg 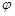= 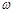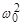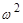^. /( - ) = tg(- 3 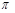/4) = 1,

звідки

= ,

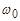оскільки

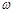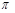= 10 , а 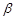= 1,6 с^-1, то 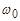= 10,5 .

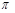Тоді рівняння власних коливань має вигляд:

x = 7 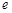^-1,6t sin10,5 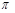t, см.

Рівняння зовнішньої періодичної сили має вигляд:

F = F₀ sin 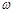t,

де

F₀ = A^.m = 72^.10^-3 Н = 72 мН.

Тоді рівняння зовнішньої періодичної сили буде мати вигляд:

F = 72 sin10 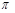t, мН.

Рекомендована література

1. Савельев И.В. Курс общей физики. - М. : Наука. 1982, т. 1, стр.17 - 245, т. 2, стр. 274 - 301.

2. Трофимова Т.И. Курс физики. - М. : Высшая школа. 1985, стр.8 - 71, 219 - 234, 243 - 252.

3. Бушок Г.Ф., Левандовський В.В., Півень В.В. Курс фізики. - К: Либідь. 2001, т.1, стор. 10 - 215.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. - М. : Наука. 1979.

5. Четров А.Г., Воробьев А.А. Задачник по физике. - М. : Высшая школа. 1981.

6. Гаркуша Т.П., Курінний В.П., Певзнер М.Ш. Збірник задач з фізики. - Київ. : Вища школа. 1995.

Контрольна робота № 1

Таблиця варіантів 1

Задачі

100. Земля обертається навколо Сонця з середньою швидкістю V_з = 29,8 км/с. Сонце рухається у напрямі до сузір'я Лебедя зі швидкі­с­тю V_с = 250 км/с. Знайти шлях і переміщення Землі за час t= 365 діб.

101. Автомобіль рухається зі швидкістю V = 72 км/год під прямим кутом до стіни. В момент, коли відстань до стіни S = 400 м, автомобіль подає короткий звуковий сигнал. Яку відстань він пройде до моменту, коли водій почує луну?

102. За проміжок часу t = 10с точка пройшла одну шосту частину кола радіуса R = 150см. Обчислити за час руху: а) середнє значення модуля швидкості; б) модуль вектора середньої швидкості; в) модуль вектора середнього повного прискорення, якщо точка рухалась зі сталим тангенціальним прискоренням, а початкова швидкість дорівнювала нулю.

103. Швидкість тіла змінюється за законом V = Аt² + Се^Вt, де А = 3 м/с³, В = с^-1, С = 1 м/с. Знайти прискорення тіла наприкінці першої секунди руху, шлях, пройдений тілом, і середню швидкість за цей же час.

104. Тіло кинуто з поверхні землі під кутом 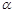=3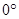до горизо­н­ту з початковою швидкістю V₀ = 10 м/с. Не враховуючи опір повіт­ря, знайти: а) швидкість тіла в момент часу t₁ = 0,8с; б) рівняння тра­єкто­рії ; в) час підйому і час спуску; г) далекість польоту; д) радіус кривизни траєкторії в момент часу t₁.

105. Знайти нормальне і тангенціальне прискорення тіла, яке кинуто з початковою швидкістю V₀ = 10 м/с під кутом 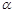= 3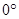до горизонту, через t₁ = 0,7с польоту. В яких точках траєкторії ці прискорення будуть найбільшими і чому дорівнюють?

106. Частинка рухається згідно з рівняннями x = kt; y = mt² + bt; z = ct², де k, m, b, c– сталі. Знайти швидкість частинки, її прискорення та модуль переміщення за перші tсекунд руху.

107. Тіло рухається згідно з рівнянням x =5sin2 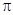ti y = 5cos2 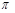t Знайти шлях, пройдений тілом за часt = 10,25с. Чому дорівнює модуль переміщення за цей час?

108. Точка рухається по колу зі швидкістю V = а₀t, де а₀ = 1 м/с². Знайти її повне прискорення після того, як вона зробить повний оберт.

109. Колесо радіуса R = 0,1мобертається так, що залежність ку­та повороту радіуса колеса від часу описується рівнянням 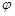= А sin Вt+ct², де А = 1 рад, В = 3 с^-1, с = 2 рад/с³. Для точок на ободі колеса знайти через t₁ = 2p/3с після початку руху: а) кутову швидкість; б) лі­нійну швидкість; в) кутове прискорення; г) тангенціальне прискорення; д) нормальне прискорення.

110. Електровоз штовхає поперед себе два вагони масами m₁ = m₂ = 60т з прискоренням а = 0,1 м/с². Коефіцієнт опору 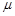= 0,005. З якою силою стиснуто пружини буферів вагонів?

111. Тіло масою m = 5кгкинуто в горизонтальному напрямку зі швидкістю V₁ = 10 м/с. Знайти: а) приріст імпульсу тіла за перші t₀ =3хв вільного падіння; б) приріст імпульсу тіла, якщо воно кинуто зі швидкі­стю V₂ = 7,9 км/с.

112. На похилій площині з кутом нахилу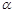= 3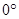лежить тіло. З яким мінімальним прискоренням треба рухати похилу площину, щоб вага тіла збільшилась вдвічі?

113. Тіло лежить на похилій площині з кутом нахилу 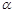. Коефі­цієнт тертя тіла на площині дорівнює f. У скільки разів мінімальна сила, з якою треба діяти на тіло, щоб витягнути його на похилу площи­ну, бі­ль­ша за силу, необхідну для утримання тіла на похилій площині?

114. Вантаж масою m = 0,5кгприв'язали до гумового шнура до­вжиною l = 40 cм, відхилили на кут 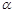= 9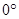і відпустили. Знайти до­вжину шнура в момент проходження вантажем положення рівноваги. Коефіцієнт жорсткості шнура k = 10³ Н/м.

115. Човен масою mрухається в стоячій воді зі швидкістю V₀. Сила опору руху F = - kV, де k – стала, що залежить від форми човна. В момент t = 0двигун було зупинено. Знайти залежність від часу шви­д­кості і шляху, який проходить човен.

116. Визначити час підйому тіла, кинутого вгору зі швидкістю V₀. Вважати, що сила опору руху F = - kV.

117. На снаряд, що вилетів з гармати, діє сила опору, внаслідок чого він рухається з прискоренням. Яку відстань пролетить снаряд, як­що його початкова швидкість V₀ = 0,8 км/с, кут нахилу вектора шви­д­кості V₀ до горизонту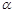= 3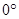, а сила опору діє в горизонтальному напрямі і спричиняє прискорення а = 0,05 м/с² ?

118. Тоненький ланцюжок масою m = 3гі довжиною l = 30cмвисить на нитці, торкаючись підлоги. Після перепалювання нитки ла­н­цю­жок впав на підлогу. Як змінювалася сила, що діяла на підлогу з бо­ку ланцюжка?

119. У шахті на глибині h₀ = 1км математичний маятник має пе­ріод коливань Т. На якій висоті над рівнем моря період коливань маятника також дорівнюватимеТ?

120. Дві кулі масами m₁ = 2кгі m₂ = 3кг рухаютьсявзаємно пер­пендикулярно зі швидкостями V₁ = 2 м/сі V₂ = 1 м/с. Визначити швидкість куль Uпісля їх зіткнення. Вважати зіткнення непружним.

121. Куля, яка рухається, пружно стикається з такою самою кулею. Удар нецентральний. Довести, що кулі розлітаються під прямим кутом одна до одної.

122. Дві шайби масами m₁ = 400гі m₂ = 200грухаються без тертя вздовж похилої площини. В момент, коли їхні швидкості відповід­но V₁= 10м/сі V₂ = 8м/с, шайби пружно стикаються. Удар централь­ний. Знай­ти швидкості шайб відразу після зіткнення.

123. Три вагонетки масами m_1, m₂і m₃ рухаються одна за одною зі швидкістями V. Як зміниться їхня швидкість, якщо з середньої ваго­нетки кинути в інші вагонетки вантажі масами m, що рухаються зі шви­дкістю Uвідносно вагонеток?

124. Куля масою m = 100гвпала з висоти h₁ = 1мна горизонтальну плиту і підскочила вгору на висоту h₂ = 0,8м. Визначити імпульс р, набутий плитою.

125. На горизонтальну поверхню вертикально падає дощ. Густи­на крапель n = 10⁴ м^-3. Маса краплі m = 50мг, швидкість - V = 10 м/с. Знайти "тиск" дощу на поверхню. Вважати, що краплі не відскакують від поверхні.

126. Снаряд масою m = 10кгмав початкову швидкість V = 800 м/с, яка спрямована під кутом 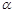= 6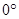до горизонту. Через деякий час після пострілу снаряд розірвався на два осколки. Один осколок мав масу m₁ = 3кг. Його швидкість через t₀ = 30сз моменту пострілу булаV₁ = 600 м/с, а кут, який вона утворювала з горизонтом, дорівню­вав нулю. Знайти швидкість другого осколка в момент часу t₀. Рух вільний, g = 10м/с².

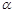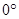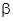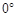127. Снаряд масою m = 10 кгмав початкову швидкість V₀ = 800м/с, яка спрямована під кутом = 3до горизонту. Через t₀ = 20спіс­ля пострілу снаряд розірвався на два осколки. Один осколок мав масу m₁ = 4кг і швидкість V₁ = 1 км/с. Вектор швидкості V₁утворювавз горизонтом кут = 4.Визначити швидкість другого осколка, як­що всі тіла рухались вільно і в одній площині. Покласти g = 10 м/с².

128. Дві кулі масами m₁ = 100гі m₂ = 200гкотяться без ковзання назустріч одна одній зі швидкістями відповідно V₁ = 1 м/сі V₂ = 2 м/с. Визначити швидкості куль після центрального пружного зіткнення. Вва­жати, що після зіткнення кулі котяться без ковзання.

129. Граната розірвалась у повітрі на Nосколків. Маса кожного i– того осколку m_і, а швидкість V_і. Знайти швидкість гранати в момент вибуху.

130. Дві краплі радіусами R₁ = 1мм іR₂ = 2ммобертаються з ку­товими швидкостями = 5 рад/сі 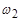= 4 рад/свідповідно, ку­тові швидкості паралельні одна одній. Визначити кутову швидкість крап­лі, що утворилась внаслідок злиття двох даних крапель.

131. Людина масою m₁ = 80кгстоїть на нерухомій платформі ма­сою m₂ = 200кг. Яку кількість обертів за хвилину робитиме платфо­рма, якщо людина рухатиметься по колу радіуса R = 5мвідносноосі обертання платформи зі швидкістю V = 7,2 км/год відносно платфор­ми? Радіус платформи R₂ = 10м. Людину вважати матеріальною точ­кою.

132. Відстань від Марса до Сонця більша за відстань від Землі до Сонця в 1,524раза. Вважаючи орбіти планет коловими, знайти, у скількі разів період обертання Марса навколо Сонця більший від пе­ріо­ду обертання Землі. З якою орбітальною швидкістю рухається Марс? Орбітальна швидкість Землі V = 29,8 км/с.

133. Обчислити роботу, що виконується на шляху S = 10мрів­номірно зростаючою з часом силою, якщо на початку руху F₁ = 10 Н, а наприкінці руху F₂ = 40 Н.

134. Автомобіль масою m = 1000кгпочинає рухатися по колу ра­діуса R = 100м з тангенціальним прискоренням 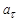= 1 м/с². Обчислити роботу двигуна, яку він виконає за один оберт автомобіля по ко­лу. Ко­ефіцієнт опору f = 0,1.

135. Функція потенціальної енергії частинки має вигляд: а) U= 2x² + 3y³ + 5z; б) U = 8xyz. Визначити силу F, що діє на частинку.

136. Функція потенціальної енергії частинки має вигляд: U(r) = 3/r - 2/r², де r– відстань від центра поля до частинки. При якому rна частинку не діятиме сила поля?

137. Тіло масою m = 1кгкинуто зі швидкістю V = 10 м/с під кутом 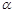= 3 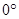до горизонту. Знайти залежність кінетичної і потенціаль­ної енергії тіла від часу. Опором повітря знехтувати.

138. На столі лежить вірьовка масою m = 1кг, завздовжки l = 2м. Якщо четверту частину (= 0,25) вірьовки звісити зі столу, то вона по­чне зісковзувати з нього. Яку роботу виконає сила тертя, що діє на ві­рьо­вку, при її повному зісковзуванні?

139. Кулька масою m = 0,01кг, що має швидкість V₁ = 500 м/с, пробиває кулю масою m = 5кг,що висить на нитці. При цьому швид­кість кульки зменшилась до V₂ = 100 м/с. Яка частина енергії кульки пе­рейшла в теплоту?

140. Знайти момент інерції тонкого однорідного кільця масою m = 200г, радіуса R = 30см: а) відносно осі, що проходить вздовж діаметра кільця; б) відносно осі, яка є дотичною до кільця.

141. До одного кінця вірьовки, перекинутої через блок, підвіше­но вантаж масою m₁ = 1кг. На другий кінець вірьовки діє сила F = at +bt³, де a = 3 Н/с, b = 3 Н/с³,t – час. Блок має форму диска масою m₂ = 3кг. З яким прискоренням рухається вантаж через t₁ = 1сі t₂ = 2свід по­чатку дії сили?

142. Трос довжиною 1м перекинуто через легкий шків, що може обертатися. Обчислити прискорення кінця троса тоді, коли один його кінець міститься вище від другого на h = 0,2м.

143. Обруч радіуса R, який обертається в горизонтальній площи­ні з кутовою швидкістю 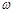, опускають на горизонтальну поверхню. Коефіцієнт тертя обруча об поверхню f. Скільки обертів зробить обруч на поверхні?

144. Циліндр масою m = 5кг і радіуса R = 10см обертається нав­коло своєї осі за законом 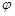= А sin 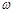t. Як залежить від часу момент си­ли, що діє на циліндр, і момент імпульсу циліндра? В які моменти часу ці величини набувають максимальних значень?

145. Куля масою m, що летить горизонтально зі швидкістю V, влучає в кулю масою m₁(m << m₁), яка лежить на гладенькій поверхні і застряє в ній. Точка зіткнення міститься у вертикальній площині, що про­ходить через центр кулі, на рівні, розміщеному нижче від центра на відстані r. Знайти кутову швидкість обертання центра кулі відно­с­но ми­т­тєвої осі, а також лінійну швидкість центра кулі після зітк­нен­ня.

146. Кулька масою m = 50гскочується без просковзування по жолобу з висоти h = 30см і робить "мертву петлю" радіуса R = 10см. З якою силою кулька тисне на опору в нижній і верхній точках петлі?

147. Визначити прискорення центра кулі, яка скочується з похилої площини. Маса кулі m = 100г, похила площина утворює з горизонтом кут 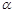= 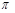/6. Чому дорівнює сила тертя, що діє на кулю, та робота цієї сили? Просковзування відсутнє.

148. Автомобіль масою m = 0,5трухається зі швидкістю V = 108 км/год. Для його зупинки ввімкнули акумулятор енергії у вигляді маховика (І = 0,5 кг^.м²). Обчислити частоту обертання маховика після зупин­ки автомомбіля.

149. На який кут треба відхилити однорідний стержень завдовж­ки l = 1м, підвішений за верхній кінець, щоб його нижній кінець при проходженні положення рівноваги мав швидкість V = 4 м/с?

150. Написати рівняння гармонічного коливального руху, якщо максимальне прискорення точки a_max= 49,3 см/с², період коливань Т= 2 с, зміщення точки від положення рівноваги у початковий момент часу х₀ = 25мм.

151. Найбільше зміщення точки, яка здійснює гармонічні коливання х_max= 10 см, найбільша швидкість V_max= 20 см/с. Знайти циклічну частоту 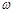коливань і максимальне прискорення a_max точки.

152. Точка здійснює коливання за законом х = А sin 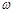t. У певний момент часу зміщення х₁точки дорівнює 5см. Якщо фаза коливань збільшилась удвічі, зміщення х₂ стало дорівнювати 8см. Знайти амплі­ту­ду А коливань.

153. Точка, що здійснює гармонічні коливання, в певний момент часу має зміщення х = 4 ^. 10^-2м, швидкість V = 5 ^. 10^-2 м/сі прискорення a = 0,8 м/с². Визначити: 1) амплітуду А і період Т коливань точки; 2) фа­зу коливань у момент часу, що розглядається; 3) максимальну швид­кість та прискорення точки; 4) час проходження шляху, що дорівнює половині амплітуди коливань при русі з положення рівноваги.

154. Точка коливається гармонічно з амплітудою А = 5смта ци­клічною частотою 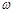= 2 с^-1, початкова фаза дорівнює нулю. Визначи­ти прискорення точки у момент часу, коли ії швидкість дорівнює 8 см/с.

155. Написати закон руху, що утворюється в результаті додава­ння двох однаково напрямлених гармонічних коливаннь, які задані рі­в­няннями: х₁ = 5^.sin(10 t + 0,75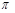); х₂ = 6^.sin(10t + 0,25 ).

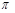156. Точка бере участь у двох коливаннях однакового напряму, які відбуваються за законами: х₁ = cos 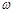t іх₂ = cos 2 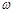t. Знайти максимальну швидкість точки.

157. Точка одночасно здійснює два гармонічні коливання, які ві­дбуваються у взаємно перпендикулярних напрямах за рівняннями: х = А₁^.sin 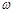tі y = А₂^.cos 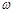t, де А₁ = 0,5см, А₂ = 2см. Знайти рівняння трає­к­торії і побудувати її у вибраному масштабі, вказавши напрям руху.

158. Точка бере участь у двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямах і описуються рівня­н­нями х = А^.sin 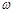t і y = А^.cos 2 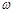t. Знайти: 1) рівняння траєкторії точки; 2) модулі швидкості і прискорення точки як функції часу.

159. Користуючись методом векторних діаграм, знайти ампліту­ду результуючого коливання при додаванні коливань х₁ = 6^.cos( 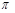t + )та х₂ = 8^.cos 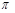t, а також визначити, у яких межах може лежати амплітуда коливання, яке виникає при додаванні двох гармонічних коливаннь однакового напряму і частоти.

160. Однорідний диск радіуса R = 30смздійснює коливання нав­коло горизонтальної осі, що проходить через: 1) одну з твірних ци­лін­д­рич­ної поверхні диска; 2) середину одного з радіусів перпендикуляр­но до площини диска. Які періоди Т₁іТ₂ його коливань?

161. Знайти закон, згідно з яким змінюється з часом натяг Fни­тки математичного маятника. Маятник коливається за законом 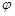= ^.cos 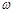t, маса його дорівнює m, довжина – l.

162. Визначити період Тколивань ртуті масою m = 121г, що зна­ходиться в U – подобній трубці. Поперечний переріз трубки S = 0,3 см².

163. Визначити період коливань тіла, що вільно рухалося б у ту­нелі, якби він проходив через центр Землі вздовж ії осі.

164. Дошка і брусок, що лежить на ній, здійснюють горизонта­льні гармонічні коливання з амплітудою А = 10см. Знайти коефіцієнт тертя між дошкою і бруском, якщо останній починає ковзати по дошці, коли її період коливань менший, ніж Т = 1с.

165. Горизонтальна платформа робить у вертикальному напрямі гармонічне коливання за законом х = а^.cos 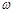t. На платформі лежить шайба з абсолютно непружного матеріалу. При якій умові шайба від­ді­лятиметься від платформи?

166. Кульку підвішено на нитці завдовжки l = 2см. Її відхи­ляють на кут 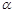= 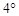і спостерігають коливання. Знайти швидкість кульки при проходженні нею положення рівноваги, вважаючи коливання незгасаючими гармонічними. Перевірити розв'зок, знайшовши швидкість кульки з рівнянь механіки.

167. Математичний маятник завдовжки l₀ = 40смі тонкий одно­рідний стержень завдовжки l = 60см здійснюють малі синхронні коли­вання навколо горизонтальної осі. Знайти відстань від центра стержня до цієї осі.

168. Айсберг у вигляді прямої призми коливається вждовж вертикальної осі. Визначити період малих коливань айсберга, якщо висота його надводної частини h = 100м.

169. До спіральної пружини підвішено тягарець, внаслідок чого пружина розтягнулась на х = 9см. Яким буде період Тколивань тягарця, якщо його відтягнути вниз, а потім відпустити?

170. Частота вільних коливань 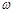= 100 с^-1, резонансна частота = 99 с^-1. Визначити добротність Qцієї системи.

171. Тонкий обруч, підвішений на цвях, забитий горизонтально в стіну, коливається у площині, паралельній стіні. Радіус Rобруча до­рівнює 30см. Обчислити період коливань обруча.

172. Однорідна пластинка, яка має форму рівнобедреного трикутника зі сторонами lі 2l, може коливатись навколо горизонтальної осі. Чому дорівнює період коливань пластинки Т, якщо вісь проходить через вершину меншого кута?

173. До спіральної пружини підвішено тягарець, внаслідок чого пружина розтягнулася на х = 9см. Яким буде період Т коливань тягарця, якщо його відтягнути вниз, а потім відпустити?

174. Тіло масою m = 1кг здійснює коливання під дією квазіпру­жної сили (k = 10 Н/м). Визначити коефіцієнт опору rв'язкого середовища, якщо період затухаючих коливань Т = 2,1с.

175. Амплітуда затухаючих коливань за час t₁ = 20с зменшилась у два рази. У скількі разів вона зменшиться за час t₂ = 1хв?

176. Знайти добротність осцилятора, у якого власна частота коливань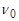= 1кГц, а час релаксації, протягом якого амплітуда коливань зменшується в еразів, 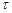= 60с.

177. Вантаж масою m = 1кг, підвішений на пружині, жорсткість якої k = 0,1 Н/м, занурений у середовище з коефіцієнтом опору r = 0,05 кг/с. Визначити добротність коливальної системи.

178. Після N = 10повних коливань точки її амплітуда коливань зменшилась від А₀ = 10см до А₁ = 6см. Коефіцієнт затухання 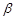= 0,2с^-1 Записати закон руху точки.

179. За час t = 100ссистема встигає зробити N = 10 коливань. За цей саме час амплітуда коливань зменшується у еразів. Чому доріню­ють: а) коефіцієнт затухання b; б) логаріфмичний декремент затухання l; в) добротність системи Q; г) відносне зменшення енергії системи за період коливань?

180. Добротність коливальної системи Q = 3, частота вільних ко­ливань 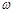= 150 с^-1. Визначити власну частоту коливань системи .

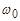181. Знайти повертаючу силу Fу момент часу t = 1ста повну енергію Wточки, що здійснює коливання за законом х= А^.cos 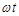, де А = 20см, 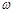= 2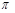/3 с^-1. Маса mматеріальної точки дорівнює 10г.

182. Кулька масою m = 0,01кгздійснює гармонічні коливання з амплітудою А = 0,03мі з частотою 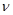= 10 с^-1. Початкова фаза коливань 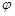дорвнює нулю. Знайти закон, за яким змінюється сила, що діє на ку­льку. Визначити: 1) повну енергію кульки; 2) значення діючої сили та відношення потенціальної енергії до кінетичної для момента часу, коли кулька відхилена від положення рівноваги на x = 0,02м.

183. Точка здійснює коливання, що описується рівнянням х = 5^.

sin2t(х- у метрах). У деякий момент часу сила F, що діє на точку, і її

по­тенціальна енергія відповідно дорівнюєють 5 мНі 0,1 мДж. Чому до­рівнюють фаза коливань і кінетична енергія точки у цей момент часу?

184. Тягар масою m = 0,1кг,підвішений на тонкій пружині, розтягує її на Dх= 0,1мм. Яку амплітуду Аматимуть коливання тягара при повній енергії W = 1 Дж?

185. Пружинний маятник вивели з положення рівноваги і відпустили. Через який час (у частинах періоду) кінетична енергія тіла, що коливається, дорівнюватиме потенціальній енергії пружини?

186. Амплітуда затухаючих коливань осцилятора за час 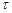= 6,93 сзменшилась у вісім разів. Як за цей час зменшилась механічна енергія осцилятора? Чому дорівнює коефіцієнт затухання?

187. Вантаж масою m = 500г,якийпідвішено до спіральної пру­жини жорсткістю k = 20 Н/м, здійснює пружні коливання у деякому середовищі. Логарифмічний декремент затухаючого коливання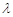= 0,004. Визначити Nповних коливань, які повинен здійснити вантаж, щоб ене­ргія коливань зменшилась у n = 2рази. За який час відбудеться це зменшення?

188. Під дією ваги електромотора балка, на якій він встановлений, угнулася на h = 1мм. При якій кількості обертів nякоря електромотора може виникнути небезпека резонансу?

189. При незмінній амплітуді змушуючої сили амплітуда вимушених коливань при частотах = 100 с^-1 і 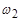= 300 с^-1 однакова. Знайти резонансну частоту .

190. Плоска гармонічна хвиля з періодом Т = 0,25сі ампліту­дою А = 3см поширюється зі швидкістю V = 240 м/с. Чому дорівнює зміщен­ня (х, t), точки, що міститься на відстані х = 60мвід джерела тоді, ко­ли від початку коливань джерела пройшов час t = 1,5с? Початкова фаза хвилі дорівнює нулю.

191. Вздовж осі Хпоширюється плоска гармонічна хвиля зі шви­д­кістю V = 20 м/с. Дві точки середовища, які містяться на відста­нях х₁ = 12мі х₂ =15мвід джерела хвиль коливаються з амплітудою А = 0,1мі з різницєю фаз 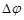= 3 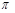/4. 1) Знайти довжину хвилі. 2) Написати рівнян­ні хвилі. 3) Знайти зміщення згаданих точок у момент часу t = 0,5с. По­чаткова фаза хвилі дорівнює нулю.

192. У скількі разів швидкість повздовжньої хвилі в міді бульша, ніж швидкість поперечної хвилі? Модуль зсуву для міді G = 12 ГПа, модуль Юнга Е = 130 ГПа.

193. Чи переносить енергію хвиля, рівняння якої (х, t) = А^.coskx^.cos 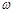t?

194. Знайти швидкість повздовжніх хвиль у: а) сталі; б) міді; в) алюмінії.

195. Визначити швидкість звуку при нормальних умовах у: а) гелії; б) азоті; в) вуглекислому газі.

196. Виразити швидкість звуку в газі через середню швидкість його молекул.

197. Знайти амплітуду незгасаючої сферичної хвилі на відстані r₂ = 15мвід точкового джерела в ізотропноиу середовищі, якщо на відстані r₁ = 3мвід нього середня густина потоку енергії <j>= 5 ГДж/м^2.c. Густина середовища = 4^.10³ кг/м³, модуль Юнга Е = 100 ГПа, частота коливань джерела 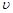= 15 кГц.

198. Пружна хвиля поширюється у мідному стержні з площею поперечного перерізу S = 3 см², що розміщенийвздовж осі Х. Знайти потік енергії через довільний переріз стержня через 1/8періоду коливань після того, як швидкість частинок середовища у цьому перерізі досягла максимального значення u_max = 35 м/с.

199. На відстані R = 3км від спостерігача з висоти h= 4кмветикально вдарила блискавка. Який час спостерігач чутиме грім від неї?