
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Установочные лекции
При первом запуске MS Project окно программы выглядит так, как показано на рис. 6. Сверху расположена строка меню, под ней панели инструментов, а ниже — рабочая область программы.
Среди панелей инструментов есть особая панель, появившаяся только в нынешней версии MS Project, — Project Guide (Консультант). На рисунке она расположена прямо над рабочей областью программы. Названия кнопок этой панели соответствуют основным объектам, с которыми можно работать в MS Project: Tasks (Задачи), Resources (Ресурсы), Track (Отслеживание) и Report (Отчет). При нажатии на любую из этих кнопок на панели в левой части рабочей области отображается список возможных действий с выбранным объектом.
Панель в левой части рабочей области, Task Pane (Область задач), также является нововведением. Она отображается после запуска MS Project и служит как Для отображения инструкций Консультанта, так и для осуществления некоторых других операций (создания новых файлов, их поиска и т. п.).

Рис. 6. Окно MS Project, открывающееся после первого запуска
Список литературы
1. Козырев А.А. Информационные технологии в экономике и управлении: Учебник. 2-е издание. – СПб.: Изд-во Михайлова В.А., 2001.
2. Автоматизированные информационные технологии в экономике: Учебник/ Под ред. проф. Г.А. Титоренко. – М.: Компьютер, ЮНИТИ, 1998.
3. Ершов Б.Л. Основы экономической информатики и вычислительной техники, ч.1,2 : Учеб. пособие, Иваново, 2002.
4. Ершов Б.Л. Программные средства офисного назначения: Учеб.пособие, Иваново, 2003
5. Ершов Б.Л. Основы информационных технологий в экономике: Учеб.пособие, Иваново, 2009
6. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
7. Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в Excel. Изд. 2-е, дополненное – М.: Информационно-издательский дом "Филинъ", 1998.
Задача №4
Имеются 1,2,…,n способов рекламирования товара, имеющих разную эффективность. Эффективность i-го способа рекламы измеряется удельным весом ui, равным отношению спроса si на товар, создаваемому этим способом, к длительности рекламы ti.
Стоимость единицы рекламы каждым способом равна р1,р2,…, рn. Фирма может себе позволить истратить на рекламу не более Z денежных единиц. Определить объемы t1,t2,…,tn рекламы каждым способом, при которых общий спрос становится максимальным. Объем рекламы любым способом является целым числом.
Опишем этот процесс уравнениями.
Объемы спроса: Объемы затрат:
S1=u1*t1 z1=p1*t1
S2=u2*t2 z2=p2*t2
… …
Sn=un*tn zn=pn*in
Общий объем спроса Общий объем затрат


Меняя объемы рекламы t1,t2,…,tn , установить максимальное значение объема спросаS, обеспечив при этом выполнение ограничений:
Объемы рекламы t1,t2,…,tn-положительные и целые числа,
Цены р1,р2,…,pn – положительные числа,
Удельный спрос u1,u2,…,un – положительные числа,
Объем затрат Z0 не превышает допустимой суммы Z.
Исходные данные
| Вид рекламы | Параметр задачи | |
| Все | Сумма S | |
| TV | Эффективность | |
| Цена | ||
| Радио | Эффективность | 0,9 |
| Цена | ||
| Местн. газета | Эффективность | 0,8 |
| Цена | ||
| Центр. газета | Эффективность | 0,95 |
| Цена |
| Вид рекламы | Объемы рекламы,t | Эффективность, ui | Стоимость, pi | Спрос, Si | Объемы затрат,zi |
| TV | |||||
| Радио | 0,9 | ||||
| Местная газета | 0,8 | ||||
| Центральная газета | 0,95 | ||||
| Сумма | |||||


Для того, чтобы не писать подробно, куда и что вводим, отобразим формулы на листе.
| Вид рекламы | Объемы рекламы,t | Эффективность, ui | Стоимость, pi | Спрос, Si | Объемы затрат,zi |
| TV | =F3*G3 | =F3*H3 | |||
| Радио | 0,9 | =F4*G4 | =F4*H4 | ||
| Местная газета | 0,8 | =F5*G5 | =F5*H5 | ||
| Центральная газета | 0,95 | =F6*G6 | =F6*H6 | ||
| Сумма | =СУММ(I3:I6) | =СУММ(J3:J6) |
Задача №8
Имеется несколько инвестиционных проектов Т1, Т2,… Т6 с приблизительно равным риском их не завершения. Для каждого проекта известна доходность вложения (D) средств и убытки (U), получаемые при провале проекта. Вы обладаете некоторой суммой S свободных средств. Необходимо подобрать оптимальное размещение средств по инвестиционным проектам. Возможные объемы вложения средств по каждому проекту превышают имеющиеся свободные средства.
Решение
В условиях неопределенного поведения проекта конфликтная ситуация инвестиций формализуется матричной игрой. Пусть первый игрок — инвестор, второй игрок — проект. Каждый из игроков имеет по 6 стратегий. Вклад в i-го проект — i-я. стратегия первого игрока, удачное завершение j проекта— j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:
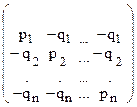
Данная задача является задачей теории игр.
Попробуем решить ее в чистых стратегиях, и если не получится , то в смешанных.
Используем критерии Вальда и Сэвиджа.
Подготовим данные для решения задачи.
Схема решения задачи следующая:
 |
Рис. 1. Схема решения задачи в смешанных стратегиях
с неизвестными вероятностями выбора вариантов
стратегии противником
На рис. 1 платежная матрица дополнена блоком расчета параметров смешанной стратегии. В столбце q поставлены весовые коэффициенты чистых стратегий в смешанной стратегии. Сумма долей S1 должна быть равна 1. Доли не меньше нуля и не больше единицы. При оптимальной стратегии суммы чисел в столбцах максимальны и равны, т.к. являются средними выигрышами игрока А.


Задача №11
Исходные данные
| Х | У |
| 25,54 | |
| 28,75 | |
| 33,58 | |
| 40,45 | |
| 47,1 | |
| 48,59 | |
| 55,97 | |
| 60,6 | |
| 63,71 | |
| 71,61 |
Задача №12
| Условие задачи | ||||||||
| Вам предлагают три варианта помещения денег в различные проекты. Длительность займа одинакова. Предусмотрен разный способ выплаты процентов. Отберите наилучший по эффективности вариант. | ||||||||
| Исходная | сумма | |||||||
| Число периодов | ||||||||
| Рассмотрим разные варианты | ||||||||
| 1-й вариант: процентная ставка | % | выплаты производятся в начале каждого периода | ||||||
| 2-й вариант: процентная ставка | % | выплаты производятся в конце каждого периода | ||||||
| 3-й вариант: процентные ставки | 0,04 | выплаты производятся в конце каждого периода | ||||||
| 0,06 | ||||||||
| 0,08 | ||||||||
| Для решения данной задачи используем | ||||||||
| финансовые функции Excel присутствуют в Пакете Анализа. | ||||||||
| Если процентная ставка меняется с течением времени, то для расчета будущего значения | ||||||||
| инвестиции после начисления сложных процентов можно использовать функцию БЗРАСПИС. | ||||||||
| Массив ставок вводим в виде диапазона чисел. Для варианта 1 и 2 используем функцию БС. | ||||||||
| В результате | ||||||||
| 1 вариант | 2 вариант | 3 вариант | ||||||
| 1 191,02р. | 1 191,02р. | 1190,592 | ||||||
| Третий вариант не подходит,можно вкладывать в первый проект или второй. |
Установочные лекции
Дата добавления: 2015-01-01; просмотров: 278; Мы поможем в написании вашей работы!; Нарушение авторских прав |