Образец задания итоговой контрольной работы №2

Вариант 1

В заданиях 1-5 вычислить интегралы, применив в 1-3, 5 – метод подстановки, в 4 – метод интегрирования по частям.

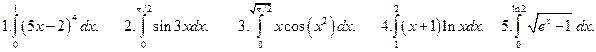
Исследовать на сходимость несобственные интегралы 6-9

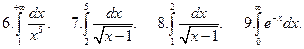
Найти площадь фигуры, ограниченной линиями (задания 10-11)

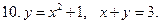
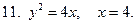
Результаты выполнения контрольной работы оцениваются по шестибалльной шкале. Оценка 0 выставляется в случае, если студент не проявил знание ключевых положений изученной темы. Оценка 1 ставится, если знания студента в области ключевых положений темы имеют фрагментарный характер. Оценка 2 ставится, если студент усвоил ключевые положения темы на уровне определений. Оценка 3 ставится, если студент усвоил ключевые положения темы на уровне определений и умеет применять при решении простейших задач. Оценка 4 ставится, если студент демонстрирует системные знания по темам контроля, но допускает значимые ошибки. Оценка ставится, если студент демонстрирует системные знания по темам контроля, но ,возможно, допускает не значимые ошибки. Положительной считается оценка 2 и выше.

Студенты, не получившие положительную оценку по результатам контроля практических умений приглашаются на консультацию для выработки мер по повышению уровня знаний. Студенты, имеющие отрицательные результаты текущего контроля, не допускаются к основному этапу итогового контроля в порядке, утвержденном кафедрой.

Общая оценка выставляется с учетом результатов всех этапов промежуточного контроля в порядке, установленном кафедрой.

7. ПРОВЕДЕНИЕ ИТОГОВОГО КОНТРОЛЯ

I семестр (зачет)

Вопросы к зачету

1. Определители. Свойства определителей.

2. Матрицы. Операции над матрицами. Обратная матрица. Ранг матрицы.

3. Решение систем линейных уравнений методом Крамера, Гаусса, матричным. Исследование систем линейных уравнений.

4. Понятие вектора. Разложение вектора по базису. Проекция вектора. Скалярное, векторное и смешанное произведение векторов.

5. Собственные числа и собственные векторы.

6. Декартова прямоугольная и полярная системы координат на плоскости.

7. Прямая на плоскости. Формы записи уравнения прямой. Угол между прямыми. Взаимное расположение прямых.

8. Кривые второго порядка: определение, классификация, характеристики.

9. Плоскость и прямая в пространстве: формы записи уравнений, взаимное расположение.

10. Понятие поверхности и линии в пространстве.

11. Понятие функции. Основные элементарные функции. Свойства функций.

12. Последовательность.

13. Предел функции в точке.

14. Предел функции на бесконечности.

15. Теоремы о пределах функции.

16. Свойство пределов, связанных с неравенствами.

17. Бесконечно малые функции. Свойство бесконечно малых функций.

18. Бесконечно большие функции. Свойство бесконечно больших функций.

19. Теорема о связи бесконечно больших и бесконечно малых функций.

20. Неопределенность (∞/∞).

21. Неопределенность (∞-∞).

22. Первый замечательный предел. Доказательство. Следствие.

23. Эквивалентные бесконечно малые величины.

24. Неопределенность (0/0).

25. Второй замечательный предел. Следствие.

26. Неопределенность (1^∞).

27. Непрерывность функции в точке. Свойства непрерывных функций.

28. Классификация точек разрыва.

29. Свойства непрерывных на отрезке функций.

30. Асимптоты графика функций.

31. Приращение функции в точке. Теорема о приращении непрерывной функции в точке.

32. Производная функции в точке.

33. Геометрический и механический смысл производной.

34. Теорема о связи непрерывной и дифференцируемой функций.

35. Таблица производных. Вывод производных элементарных функций.

36. Основные теоремы: о производных суммы, произведения частного, сложной и обратной функций.

37. Производные высших порядков.

38. Первая и вторая производные параметрически заданной функции.

39. Дифференциал функции и его свойства.

40. Основные теоремы дифференциального исчисления: теорема Ролля, теорема Лагранжа (доказательство), теорема Лопиталя.

41. Условия монотонности функции.

42. Точки экстремума. Необходимое условие существования точек экстремума. Критические точки.

43. Достаточное условие существования экстремума.

44. Выпуклость графика функции.

45. Условие выпуклости графика функции.

46. Точки перегиба. Необходимое условие существования точек перегиба. Критические точки.

47. Достаточное условие существования точек перегиба.

48. Наибольшее и наименьшее значения функции непрерывной на отрезке.

49. Полная схема исследования функции.

II семестр (экзамен)

Вопросы к экзамену

1. Первообразная. Теорема о множестве всех первообразных (доказательство).

2. Неопределенный интеграл. Свойства неопределенного интеграла.

3. Таблица неопределенных интегралов.

4. Замена переменной в неопределенном интеграле.

5. Интегрирование по частям в неопределенном интеграле. Основные классы интегрируемых по частям функций.

6. Интегрирование квадратичных трехчленов.

7. Интегрирование рациональных дробей. Простейшие дроби. Разложение правильной дроби на простые дроби.

8. Интегрирование неправильной дроби.

9. Интегрирование иррациональных выражений.

10. Интегрирование тригонометрических выражений.

11. Универсальная тригонометрическая подстановка.

12. Определенный интеграл. Геометрический смысл. Свойства определенных интегралов. Формула Ньютона-Лейбница.

13. Замена переменной и интегрирование по частям в определенном интеграле.

14. Вычисление площадей плоских фигур.

15. Несобственный интеграл I рода. Несобственный интеграл II рода.

16. Обыкновенные дифференциальные уравнения. Дифференциальные уравнения I порядка. Задача Коши.

17. Дифференциальные уравнения с разделяющимися переменными.

18. Однородные дифференциальные уравнения 1-го порядка и приводящиеся к ним.

19. Линейные дифференциальные уравнения I порядка, метод Бернулли.

20. Дифференциальные уравнения высших порядков допускающие понижение порядка.

21. Линейные однородные дифференциальные уравнения II порядка с постоянными коэффициентами.

22. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости.

23. Достаточные признаки сходимости знакоположительных рядов.

24. Знакопеременные ряды. Теорема. Лейбница.

25. Степенные ряды. Теорема Абеля. Интервал сходимости. Радиус сходимости.

26. Ряд Тейлора и Маклорена. Разложение функции в ряд Тейлора.

27. Приложение рядов Тейлора.

28. Пространство элементарных событий. Алгебра событий.

29. Классическая вероятность. Статистическая вероятность.

30. Основные теоремы о вероятностях случайных событий.

31. Условная вероятность. Формула полной вероятности. Формула Бейеса.

32. Схема Бернулли. Повторные независимые испытания..

33. Формулы Бернулли, Лапласа, Пуассона.

34. Дискретные случайные величины. Функция распределения. Числовые характеристики и их свойства.

35. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма. Эмпирическая функция распределения. Выборочная средняя и дисперсия.

Критерии оценки зачета и экзамена

Ответ студента на экзамене оценивается одной из следующих оценок: «отлично», «хорошо», «удовлетворительно», «неудовлетворительно», которые выставляются по следующим критериям.

Оценки «отлично» заслуживает студент, обнаруживший всестороннее, систематическое и глубокое знание учебного и нормативного материала, умеющий свободно выполнять задания, предусмотренные программой, усвоивший основную и знакомый с дополнительной литературой, рекомендованной кафедрой. Как правило, отличная оценка выставляется студентам, усвоившим взаимосвязь основных понятий курса, их значение для приобретаемой профессии, проявившим творческие способности в понимании, изложении и использовании учебного материала, знающим точки зрения различных авторов и умеющим их анализировать.

Оценка «хорошо» выставляется студентам, обнаружившим полное знание учебного материала, успешно выполняющим предусмотренные в программе задания, усвоившим основную литературу, рекомендованную кафедрой. Этой оценки, как правило, заслуживают студенты, демонстрирующие систематический характер знаний по дисциплине и способные к их самостоятельному пополнению и обновлению в ходе дальнейшей учебной работы и профессиональной деятельности.

На «удовлетворительно» оцениваются ответы студентов, показавших знание основного учебного материала в объеме, необходимом для дальнейшей учебы и в предстоящей работе по профессии, справляющихся с выполнением заданий, предусмотренных программой. Как правило, оценка «удовлетворительно» выставляется студентам, допустившим погрешности в ответе на экзамене и при выполнении заданий, не носящие принципиального характера, когда установлено, что студент обладает необходимыми знаниями для последующего устранения указанных погрешностей под руководством преподавателя.

Оценка «неудовлетворительно» выставляется студентам, обнаружившим пробелы в знаниях основного учебного материала, допускающим принципиальные ошибки в выполнении предусмотренных программой заданий. Такой оценки заслуживают ответы студентов, носящие несистематизированный, отрывочный, поверхностный характер, когда студент не понимает существа излагаемых им вопросов, что свидетельствует о том, что студент не может дальше продолжать обучение или приступать к профессиональной деятельности без дополнительных занятий по соответствующей дисциплине.

8. ПЕРЕЧЕНЬ ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ УЧЕБНОЙ ЛИТЕРАТУРЫ, НЕОБХОДИМОЙ ДЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ (МОДУЛЯ)

а) основная литература

1. Шипачев, В. С. Высшая математика: 8-е изд., пер. и доп. Учебник и практикум / В. С. Шипачёв. - М.:Издательство Юрайт, 2014. - 447 с.

2. Индивидуальные задания по высшей математике: учеб. пособие в 3 ч. / А. П. Рябушко, В. В. Бархатов, В. В. Державец, И. Е. Юруть; под ред. А. П. Рябушко. - Минск: Вышэйшая школа, 2010.- 262 с.

б) дополнительная литература

1. Шнейдер В. Е. и др. Краткий курс высшей математики, тт. 1. - М.: Высшая школа, 1978.- 256 с.

2. Шнейдер В. Е. и др. Краткий курс высшей математики, тт. 2. - М.: Высшая школа, 1978.- 240 с.

3. Гмурман, В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. - М.: Высшее образование, 2006.- 240 с.

4. Гмурман, В. Е. Руководство по решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. - М.: Высшее образование, 2008. - 240 с.

5. Краснов М. Л. и др. Вся высшая математика, т.1. - М.: Эдиториал, 2000. – 340 с.

6. Вентцель, Е. С. Теория вероятностей и ее инженерные приложения: учеб. пособие / Е. С. Вентцель. - М.: Высш. шк., 2000. – 360 с.

9. ПЕРЕЧЕНЬ РЕСУРСОВ ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАТИВНОЙ СЕТИ «ИНТЕРНЕТ», НЕОБХОДИМЫХ ДЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ (МОДУЛЯ)

программное обеспечение не предусмотрено

базы данных, информационно-справочные и поисковые системы:

http://www.kgu.edu.ua Поисковая система «Ирбис».

http://ru.wikipedia.orgВикипедия;

www.newlibrary.ru - новая электронная библиотека;

www.edu.ru – федеральный портал российского образования;

www.mathnet.ru – общероссийский математический портал;

www.elibrary.ru – научная электронная библиотека;

www.matburo.ru – матбюро: решения задач по высшей математике;

www.nehudlit.ru - электронная библиотека учебных материалов.