
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение законов распределения наработки на отказ
Важное значение имеет правильный подбор вида теоретического закона распределения случайной величины. Каждым из известных стандартных распределений, экспоненциальным, нормальным, Вейбулла и др., охватывается довольно узкий круг эмпирических распределений. Между тем эти законы хорошо изучены и с достаточной точностью описывают статистические функции распределения случайных величин различного класса.
Существуют в то же время универсальные методы выравнивания статистических рядов. Например, имеется специально разработанная система кривых Пирсона, которые зависят в общем случае от четырех параметров. При выравнивании этих кривых параметры выбираются с таким расчетом, чтобы сохранить первые четыре вида статистического распределения (математическое ожидание, дисперсию, третий и четвертый моменты). Известны также набор кривых распределения Н.А. Бородачева, функции Джонсона и другие методы.
Практика показала, что с такими функциями работать довольно сложно, а результаты выравнивания невсегда бывают положительными. Поэтому лучше выбрать некоторый круг стандартных распределений и по какому-либо критерию находить функцию, наиболее точно согласующую теоретический и статистический законы распределения.
Практически подавляющее большинство статистических распределений, можно описать одним из пяти стандартных распределений:
1. Нормальным

где х – возможное значение случайной величины Х; f(х) – функция плотности распределения; m – математическое ожидание; D – дисперсия.
2. Логарифмически-нормальным
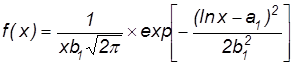 ,
,
где а1, b1 – параметры закона распределения.
3. Гамма-распределением
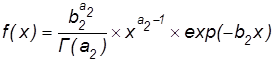 ,
,
где Г(а2) – гамма-функция а2.
4. Распределением Вейбулла
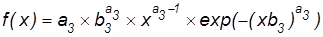 ,
,
5. Равномерным распределением
 |
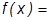
|

Оценки математического ожидания m и дисперсии D случайной величины Х (время безотказной работы или время восстановления) вычисляются по формулам:

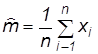 ,
,
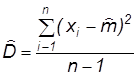 ,
,
где х1, х2, …,хi,…,хn - совокупность n результатов наблюдений над случайной величиной Х. Оценки параметров а1,…,а4 и b1,…,b4 стандартных законов распределения вычисляют подстановкой найденных оценок 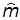 и
и 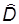 в выражение параметров теоретических распределений через математическое ожидание и дисперсию [1] (табл. 1).
в выражение параметров теоретических распределений через математическое ожидание и дисперсию [1] (табл. 1).
Таблица 1
| Закон распределения | Расчетная формула | |
| Для первого параметра | Для второго параметра | |
| Логарифмически-нормальное | 
| 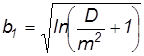
|
| Гамма-распределение | 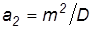
| 
|
| Распределение Вейбулла | решить относительно параметра а3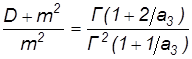
| 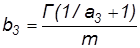
|
| Равномерная плотность распределения | 
| 
|
Экспериментальная оценка надежности может быть получена по экспериментальным данным об отказах. Эта статистика может собираться в процессе эксплуатации или в результате специальных испытаний на надежность системы. Показатели надежности систем могут быть вычислены по данным об отказах элементов или систем в целом. Это наиболее полная и достоверная оценка, так как аппаратура находится в реальных условиях работы. Теоретические же методы дают приближенную оценку ожидаемого уровня надежности.
Испытания на надежность делятся на определительные и контрольные.
– определительные – испытания, в результате которых определяются фактические показатели надежности системы. Для чего необходима большая статистическая выборка по отказам.
– контрольные – испытания, на основе которых не определяются фактические значения, а проверяются статистические гипотезы и по ним принимается решение: удовлетворяет система заданным требованиям по надежности или нет.
Для проведения испытания составляются планы испытаний, в которых задаются характеристики:
– число систем, поставленных на испытание – N;
– порядок замены отказавших систем в процессе испытаний: Б – без замены отказавших систем на новые; В – с заменой отказавших систем на новые;
– продолжительность испытаний. Они могут продолжаться до отказа установленного количества систем r<N или заданный интервал времени Т. Есть план, когда испытания ведутся до отказа r систем, если наработка tr до появления r-го отказа tr<T, или продолжаются определённое время Т, если tr≥T.
По результатам испытаний формируется вариационный ряд наработок на отказ 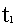
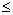
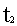
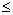

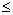 …
… 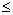
 (t1 – отказ 1-й системы, t2 – отказ 2-й системы и т.д.). По ним подсчитывают суммарную наработку на отказ в зависимости от принятого плана испытаний. Рассмотрим возможные планы испытаний:
(t1 – отказ 1-й системы, t2 – отказ 2-й системы и т.д.). По ним подсчитывают суммарную наработку на отказ в зависимости от принятого плана испытаний. Рассмотрим возможные планы испытаний:
План: N,Б,r
 ,
,
где Т∑r – суммарная наработка на отказ, через которую можно определить статистическую оценку показателей безотказности, например:
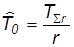 .
.
План: N,B,r
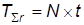 .
.
План: N,Б,T
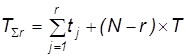 .
.
План: N,В,T
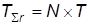 .
.
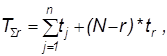 План: N,Б,(r,T)
План: N,Б,(r,T)
| |||
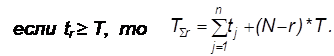 |
План: N,В,(r,T)
 | |||
 |
Дата добавления: 2015-01-05; просмотров: 547; Мы поможем в написании вашей работы!; Нарушение авторских прав |