Статистические методы контроля надёжности серийных систем

Среди планов испытаний выборочного контроля выделяют:

– планы типа однократной выборки,

– планы типа двукратной выборки,

– последовательный контроль надежности.

В планах типа однократной выборки из общего количества N выпускаемых изделий выбирается n изделий и каждое подвергается контролю на надежность. Находится число дефектных изделий среди n изделий. Число дефектных изделий в выборке n – d(n). Приемочное число с – граничное число дефектных изделий определяется на базе оперативной характеристики. Если d(n) < c, то партия принимается, а если d(n) > c – партия бракуется.

Если выполняется n ≥ 0,1,…,N, то можно принимать биноминальный закон распределения. Строится оперативная характеристика П(q), где

.

Биноминальный закон распределения:

,

где С – приёмочное число; Сn_i – число сочетаний из n по i.

В планах типа двукратной выборки из общего числа изделий N выбирается n₁ изделий (n₁ > N). Эта выборка подвергается контролю на надежность и подсчитывается число дефектных изделий в n₁. Если d(n₁) ≤ c₁, то партия принимается, d(n₁) > c₂ – партия бракуется. c₁ < d(n₁) ≤ c₂ – зона неопределенности. Берется вторая выборка n₂, такая, что (n₁ + n₂ < N) и подвергается контролю на надежность. Если d(n₁ + n₂) ≤ c₃ – партия принимается, d(n₁ + n₂) > c₃ – партия бракуется. Возможен вариант, когда c₂ = c₃.

Оперативная характеристика П(q) = Ра₁ + Ра₂, где Ра₁ и Ра₂ –несовместимые события (рис. 3.3).

Событие а₁: d(n₁) < c₁; а₂: d(n₁ + n₂) ≤ c₂; d(n₁) > c₁

Партия изделий будет принята, если наступит одно из несовместных событий:

– а₁: для первой выборки выполняется условие

– а₂: для двух последних выборок выполняются условия

,

Тогда оперативная характеристика

,

где Ра₁ – вероятность события а₁, Ра₂ – вероятность события а₂.

Ра₁ вычисляется по формуле одновыборочного контроля, а Ра₂

Рис. 3.3 Графическая иллюстрация плана двукратной выборки

При последовательном контроле надежности берется целый ряд выборок и каждый раз сравнивается с приемочными числами. Необходимо, чтобы было соблюдено условие (n₁ + n₂+…+n_i) ≤ N. Если d(n₁ + n₂+…+n_i) = d_i. Тогда возмём выборку n₁, подсчитаем d(n₁) и сравним с передаточными числами. Если d₁ ≤ c₁ – партия принимается, d₁ > c₁’ – партия бракуется. c₁ < d(n₁) ≤ c₁’ – зона неопределенности. Необходимо взять выборку n₂ и подсчитать d₂. Если d₂ ≤ c₂ – партия принимается, d₂ > c₂’ – партия бракуется. c₁ < d(n₁) < c₂’ – зона неопределенности. Берём выборку n3 и так далее…Выборка n_i. Если d_i < c_i – партия принимается, d_i > c_j’– партия бракуется;

Последовательный контроль надежности проводится по накопленному числу дефектных изделий r = 1, 2, 3,… или по суммарной наработке на отказ Т_∑r в зависимости от плана испытаний. В основе принятия решений лежит вероятность gr – отношение правдоподобия, r = 1,2,3,… которая и сравнивается с величинами риска поставщика и потребителя. Если

– продолжается испытание,

– партия принимается,

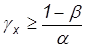– партия бракуется.

Рассмотрим практическую методику последовательного контроля надежности по суммарной наработке на отказ Т_Sr (рис. 3.4).

– испытание продолжается,

– партия принимается,

– партия бракуется.

Рис. 3.4 Использование последовательного контроля надёжности

,

,

Т₀₁ – средняя наработка на отказ исправной системы по ее паспортным данным, Т₀₂ – средняя наработка на отказ системы, которую считают надежной

.

Примеры решения задач