
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матриця повних зв’язків та методи її визначення
На основі наведених даних таблиці 1.11. дати оцінку рівня конкурентоспроможності потенціалів фармацевтичних фірм «Дарниця» та «Bayer».
Таблиця 1.11.
Основні характеристики підприємств (станом на початок 2003 року)
| Показник | Дарниця | Вауеr |
| Рік заснування | ||
| Обсяг продажу, млн. дол. | ||
| Чистий прибуток, млн. дол. | 3,1 | |
| Кількість працівників, чол. | ||
| Кількість філій, один. | - | |
| Країна | Україна | Німеччина |
Модуль 1. Теоретико-множинне визначення системи. Методи опису та характеристики систем
Лекція № 3. Графоаналітичний метод опису ТС
Матриця повних зв’язків та методи її визначення
Найбільш поширеним є графоаналітичний опис ТС, коли граф  зображують у вигляді матриці суміжності.
зображують у вигляді матриці суміжності.
Матрицею суміжності (зв’язності, безпосередніх зв'язків) називають матрицю А розміром  , де
, де  – кількість вершин графа, елементи якого
– кількість вершин графа, елементи якого  мають значення 1, якщо з вершини
мають значення 1, якщо з вершини  можна безпосередньо перейти у вершину
можна безпосередньо перейти у вершину  , і значення 0 – у протилежному випадку, тобто
, і значення 0 – у протилежному випадку, тобто
 (1)
(1)
Елементи  при
при  виражають зв’язність окремих ребер усередині
виражають зв’язність окремих ребер усередині  -ї вершини. Зазвичай вони мають нульові значення, але якщо в матриці суміжності діагональний елемент дорівнює 1, то це означає, що відповідна вершина має петлю. Петля – це ребро, що виходить з вершини й веде в ту саму вершину.
-ї вершини. Зазвичай вони мають нульові значення, але якщо в матриці суміжності діагональний елемент дорівнює 1, то це означає, що відповідна вершина має петлю. Петля – це ребро, що виходить з вершини й веде в ту саму вершину.
Для розглянутої раніше системи автоматичного регулювання температури, граф якої зображений на рис. 1, матриця А має вигляд
 .
.
 |
Рис. 1. Граф системи автоматичного регулювання температури
На основі аналізу матриці можна зробити наступні висновки:
- порядок (ступінь) матриці А дорівнює кількості вершин графа N;
- для орієнтованого або змішаного графа матриця суміжності несиметрична;
- сума елементів кожного рядка матриці А виражає кількість зв'язків цієї вершини з іншими вершинами;
- для неорієнтованого графа (рис. 2) матриця суміжності буде симетричною відносно головної (лівої) діагоналі:
 .
.

Рис. 2. Схема неорієнтованого графа  .
.
Матричне зображення структури ТС дає можливість застосовувати комп’ютерну техніку для аналізу системи, саме тому воно є дуже розповсюдженим.
Уведемо ще кілька понять графоаналітичного опису ТС.
Шляхом називають послідовність ребер, коли кінець попереднього ребра збігається з початком наступного ребра; його довжину визначають кількістю ребер, з яких складається цей шлях.
| Приклад | Для системи, структуру якої зображено на рис. 6, послідовність 1-2, 2-3, 3-4 шляхом графа від першої до четвертої вершини, а довжина шляху 1-2-3-4 дорівнює трьом. |
Неважко помітити, що матриця суміжності є матрицею шляхів графа, довжина яких дорівнює одиниці. Саме тому матрицю суміжності  називають матрицею безпосередніх зв'язків. Для того щоб одержати матрицю шляхів довжини 2, необхідно матрицю суміжності піднести до квадрата. У загальному випадку має місце таке твердження: загальну кількість n транзитних шляхів з вершини i у вершину j довжиною k можна отримати підняттям матриці А до k-го ступеню.
називають матрицею безпосередніх зв'язків. Для того щоб одержати матрицю шляхів довжини 2, необхідно матрицю суміжності піднести до квадрата. У загальному випадку має місце таке твердження: загальну кількість n транзитних шляхів з вершини i у вершину j довжиною k можна отримати підняттям матриці А до k-го ступеню.
Елемент  матриці
матриці 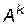 визначає кількість шляхів довжиною
визначає кількість шляхів довжиною  з вершини i у вершину j.
з вершини i у вершину j.
Структура ТС є повнозв’язною, якщо 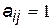 при
при  , тобто якщо всі елементи матриці
, тобто якщо всі елементи матриці 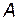 дорівнюють 1, крім тих, що розташовані на головній її діагоналі. У протилежному випадку ТС є неповнозв’язною. Очевидно, що має сенс кількісне оцінювання зв’язності при неповнозв’язності структури графа
дорівнюють 1, крім тих, що розташовані на головній її діагоналі. У протилежному випадку ТС є неповнозв’язною. Очевидно, що має сенс кількісне оцінювання зв’язності при неповнозв’язності структури графа  .
.
Повнозв’язана структура (інші назви -- структура з повним з'єднанням, кільце з повним з'єднанням хордам – Chordal Ring, повний граф, топологія максимального групування) зображена на рис. 3.

Рис. 3. Структура з повним з'єднанням
Таким чином, будь-яка структура ТС, виражена орієнтованим (або змішаним) графом, є неповнозв’язною. Дійсно, для орієнтованого ребра графа елемент матриці зв’язності 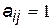 , а елемент
, а елемент  . Отже, нулю в такій матриці дорівнюють не тільки елементи головної діагоналі.
. Отже, нулю в такій матриці дорівнюють не тільки елементи головної діагоналі.
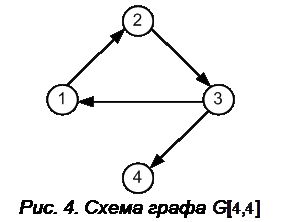
Контур – це шлях, у якому початкова і кінцева вершини графа збігаються. Так, на графі, зображеному на рис. 4, шлях 1-2-3-1 є контуром. Наявність контурів можна визначити, скориставшись матрицею повних зв'язків.
Матрицею повних зв'язків називають матрицю  розміром
розміром 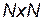 , для елементів якої виконуються наступні умови:
, для елементів якої виконуються наступні умови:
 , якщо існує хоча б один шлях, що веде з i-ї вершини в j-ту;
, якщо існує хоча б один шлях, що веде з i-ї вершини в j-ту;
 , якщо такого шляху не існує.
, якщо такого шляху не існує.
Якщо діагональний елемент матриці С дорівнює одиниці, то для цієї i-ї вершини існує контур.
 Матрицю повних зв'язків можна визначити двома способами: матричним або графічним.
Матрицю повних зв'язків можна визначити двома способами: матричним або графічним.
Матричний метод базується на наведеному вище твердженні, що матриця  визначає кількість n шляхів довжиною k з вершини i у вершину j. Якщо додати матриці
визначає кількість n шляхів довжиною k з вершини i у вершину j. Якщо додати матриці  (
(  ), тобто знайти
), тобто знайти
 (2)
(2)
то елемент  цієї матриці буде характеризувати кількість шляхів від 1 до n з вершини i у вершину j. Визначимо елементи матриці повних зв’язків таким чином:
цієї матриці буде характеризувати кількість шляхів від 1 до n з вершини i у вершину j. Визначимо елементи матриці повних зв’язків таким чином:
 (3)
(3)
Приклад. Для структури, зображеної графом  (див. рис. 4), матричним методом скласти матрицю повних зв’язків, яка характеризує наявність шляхів від 1 до 3 для кожної вершини.
(див. рис. 4), матричним методом скласти матрицю повних зв’язків, яка характеризує наявність шляхів від 1 до 3 для кожної вершини.
Відповідно до виразу (2) знайдемо матрицю  при
при  :
:
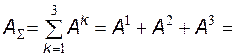

Згідно з правилом (3) матриця повних зв’язків матиме такий вигляд:

Отже, для вершин 1, 2 і 3 цього графа існує контур, який вже було знайдено раніше для вершини 1 під час аналізу графічної структури системи.
Алгоритм множення матриць пояснюється рис. 5.
|

Рис. 5. Алгоритм множення матриць
Графічний метод базується на побудові дерева шляхів від вершини і до всіх інших вершин. Кожну гілку дерева шляхів будують до першого повторення вершини. Якщо шлях від і-ї вершини до  -ї існує, то
-ї існує, то  , у протилежному випадку
, у протилежному випадку  . Приклад побудови дерева шляхів для вершини 1 графа
. Приклад побудови дерева шляхів для вершини 1 графа  (див. рис. 4) поданий на рис. 6.
(див. рис. 4) поданий на рис. 6.

Рис. 6. Дерево шляхів для вершини 1 графа G[4,4]
Дата добавления: 2015-01-05; просмотров: 379; Мы поможем в написании вашей работы!; Нарушение авторских прав |
