
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВАРІАНТ 18
Частина перша
| А | Б | В | Г | А | Б | В | Г | А | Б | В | Г | |||||
| 1.1 | X | 1.5 | X | 1.9 | X | |||||||||||
| 1.2 | X | 1.6 | X | 1.10 | X | |||||||||||
| 1.3 | X | 1.7 | X | 1.11 | X | |||||||||||
| 1.4 | X | 1.8 | X | 1.12 | X |
1.1.  Відповідь. Б.
Відповідь. Б.
1.3. Заміна 


 - не підходить.
- не підходить.

 Відповідь. В.
Відповідь. В.
1.5. 
 Відповідь. В.
Відповідь. В.
1.6. 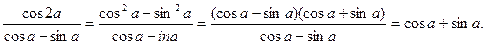
Відповідь. Б.
1.8. 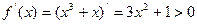 для всіх
для всіх  . Відповідь. А.
. Відповідь. А.
1.10. 
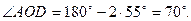
 як вертикальні. Відповідь. В.
як вертикальні. Відповідь. В.
1.12. Діагональ прямокутника не може бути меншою від сторони прямокутника, тому дана діагональ знаходиться в одній площині зі стороною 3 см. За теоремою Піфагора, знайдемо іншу сторону цього прямокутника, яка і буде висотою паралелепіпеда:  .
.
 Відповідь. Г.
Відповідь. Г.
Частина друга
2.1.  Відповідь. 5.
Відповідь. 5.
2.2. Кількість способів дорівнює 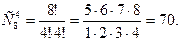 Відповідь. 70.
Відповідь. 70.
2.3. Знайдемо точки перетину графіків функцій 
і 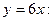
 ;
; 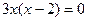 ;
;  ,
,  .
.
Зобразимо схематично графіки на рисунку.
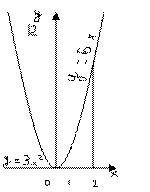
Шукана площа  (кв. од).
(кв. од).
Відповідь. 4 кв. од.
2.4. 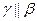 , а тому
, а тому  Отже,
Отже,  , за двома кутами:
, за двома кутами:  спільний,
спільний,  як внутрішні різносторонні при паралельних прямих
як внутрішні різносторонні при паралельних прямих  і
і 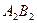 . Отже,
. Отже,  ;
;  (см).
(см).
 Відповідь. 6 см.
Відповідь. 6 см.
Частина третя
3.1.Маємо: 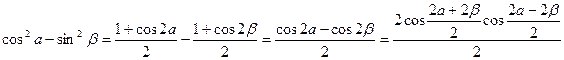 =
=
 , що й треба було довести.
, що й треба було довести.
3.2. 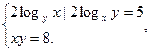 Нехай
Нехай  , тоді
, тоді  Маємо з першого рівняння:
Маємо з першого рівняння: 



Тоді: 1) 



2) 


 Відповідь. (4; 2), (2; 4).
Відповідь. (4; 2), (2; 4).
3.3. На рисунку зображено піраміду QABC, задану в умові. QAB  ABC; QK- висота піраміди; QK належить грані QAB.
ABC; QK- висота піраміди; QK належить грані QAB.
За умовою, 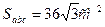 ,
, 
Позначимо AB = AC = BC = a. Тоді 36 
a = 12 (см).

Нехай КМ  АС, тоді за теоремою про три перпендикуляри, QM
АС, тоді за теоремою про три перпендикуляри, QM  AC, а тому
AC, а тому 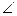 QMK – кут, що утворює бічна грань QAC із площиною основи;
QMK – кут, що утворює бічна грань QAC із площиною основи; 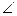 QMK = 45
QMK = 45 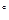 .
.
 (за катетом і протилежним кутом), тому КN = KM.
(за катетом і протилежним кутом), тому КN = KM.
 (за катетом протилежним кутом), тому АК = КВ =
(за катетом протилежним кутом), тому АК = КВ =  , тобто К – середина АВ.
, тобто К – середина АВ.
У 

У 
Аналогічно, NQ = 
Тоді 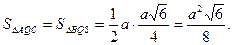
Площа бічної поверхні :
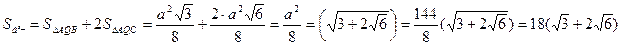
Відповідь.  см.
см. 
| а | б | в | г | |
| 1.5 | Х | |||
| 1.6 | Х | |||
| 1.7 | Х | |||
| 1.8 | Х |
Дата добавления: 2015-01-05; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |