Вектордың скаляр көбейтіндісі

Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады: .

Тік бұрышты декарт координаталар жүйесінде векторының басы мен соңының координаталары белгілі болсын 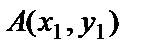және . Сонда векторын координаталары арқылы былай жазуға болады: = векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес. Жазықтықта вектордың координатасын екі сан анықтаса, айталық , кеңістікте үш сан анытайды, .

Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең: . және векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады: .Ал векторын санға көбейту мынадай түрде анықталады: . және векторларының скаляр көбейтіндісі мынадай:

7. Жазықтықтағы түзудің теңдеулері. Жазықтықтағы түзу (1-сурет) Оу осін В(0;b) нүктесінде қиып, Ох осімен (0< < ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған бұрышының тангенсін ВМК үшбұрышынан табамыз:

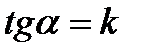; деп белгілеп, түзудің бұрыштық коэффициентідеп атау қабылданған. Сонымен: .

Осы қатынастан у-ті тапсақ: y=kx+b (2)

Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды. (2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады. Дербес жағдайларын қарастырайық.

1. Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді (2-сурет)

2. Егер болса, онда болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.

3. Егер болса, онда мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.

Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі Ах+Ву+С=0 (3)

Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды.

(3) теңдеуді әдетте түзудің жалпы теңдеуі деп атайды

8. Функцияның нүктедегі шегі. Тамаша шектер Анықтама.Егер алдын ала берілген, мейілінше аз санына саны табылып, шартын қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады да, былай жазылады: .Анықтамадағы теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: . интервалды нүктесінің -маңайы дейді. Сол сияқты теңсіздікті ашсақ: . интервалды А нүктесінің -маңайы дейді.