
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кері функцияның туындысы
y=f(x) функциясына кері функция (x=f - 1(y)) туындысы:  .
.
11. Функцияның дифференциалы және жуықтап есептеуге қолдану. Мысалдар. Функцияның дифференциалы.  функциясының шектелген туындысы бар болсын, онда:
функциясының шектелген туындысы бар болсын, онда:  , демек
, демек 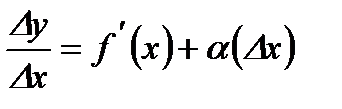
 шексіз аз шама.
шексіз аз шама.
Онда функцияның өсімшесі былай жазылады:  . Осы теңдікте екінші қосылғыш
. Осы теңдікте екінші қосылғыш  ,
, 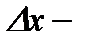 ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш
ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш  ке эквивалентті шама болады.
ке эквивалентті шама болады.
Анықтама.Функцияның туындысының аргументтің өсімшесіне көбейтіндісін дифференциал деп атайды және мына түрде жазады:  . Дербес жағдайда, егер
. Дербес жағдайда, егер 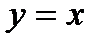 болса, онда
болса, онда 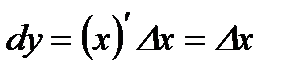 , осыдан
, осыдан  және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:
және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:  . Осыдан
. Осыдан  , яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
, яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
Дифференциалды есептеу ережесі.Айталық  және
және  дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
1)  , мұндағыс –сан.
, мұндағыс –сан.
2)  ,
,
3)  , егер
, егер  .
.
4) Егер функциясы
функциясы 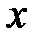 нүктесінде дифференциалданатын, ал
нүктесінде дифференциалданатын, ал
 нүктесінде дифференциалданатын болса, онда
нүктесінде дифференциалданатын болса, онда  күрделі функция үшін,
күрделі функция үшін,  . Бұл ережені бірінші дифференциал формасының инварианттығы деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,
. Бұл ережені бірінші дифференциал формасының инварианттығы деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,  функциясы дифференциалданатын болсын, онда оның өсімшесі:
функциясы дифференциалданатын болсын, онда оның өсімшесі:
 , осыдан
, осыдан  .
.
Егер  нүктесінде функцияның мәні берілсе, онда:
нүктесінде функцияның мәні берілсе, онда: 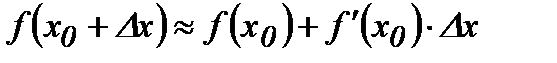 .
.
мысал.  -ты жуықтап есепте.
-ты жуықтап есепте. 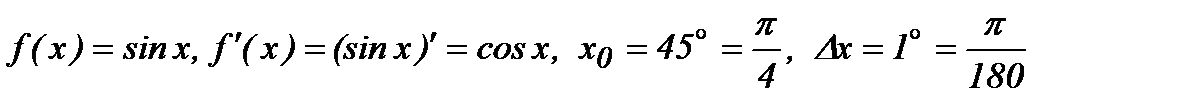
 .
.
12. Лопиталь ережесі арқылы анықталмағандықты ашу.Теорема (Лопиталь ережесі). f(x) және g(x) функциялары  (
( 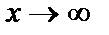 ) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады:
) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады:  .Лопиталь ережесін қолданып ектерді есмептейік.
.Лопиталь ережесін қолданып ектерді есмептейік.
1.  .
.
2.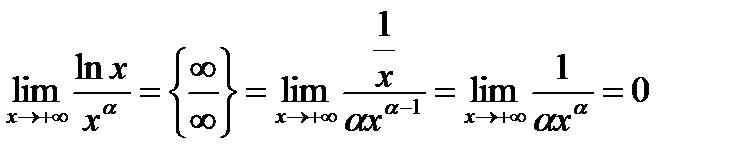
3.  .
.
Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен  түріндегі анықталмағандықты
түріндегі анықталмағандықты  немесе
немесе  түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х2 бөлімнің бөліміне түсірілді.
түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х2 бөлімнің бөліміне түсірілді.
4.  . Айталық
. Айталық 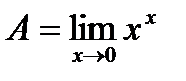 деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейік:
деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейік: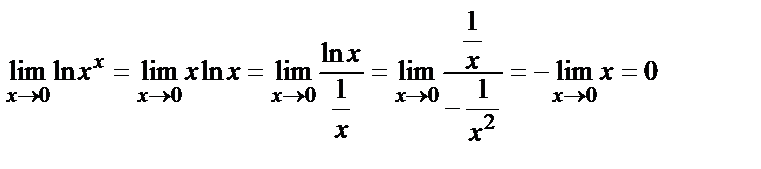
Дата добавления: 2015-01-05; просмотров: 779; Мы поможем в написании вашей работы!; Нарушение авторских прав |