
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Асимптота
Анықтама.Егер y=f(x) функциясы үшін 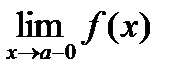 және
және  шектерінің ең болмағанда біреуі шексіздікке тең болса, онда
шектерінің ең болмағанда біреуі шексіздікке тең болса, онда 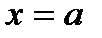 функция графигінің тік асимптотасы деп аталады (6а-сурет). у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).
функция графигінің тік асимптотасы деп аталады (6а-сурет). у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).
Көлбеу асимптотаның дербес жағдайы (k=0) горизонталь асимптота болады: y=b
Көлбеу асимптотаны мынадай теорема көмегімен табуға болады.
Теорема. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы болуы үшін мынадай шектердің бар болуы қажетті және жеткілікті: 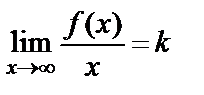 ,
, 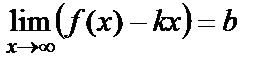 .
.
15. Анықталмаған интеграл және оның қасиеттері.Анықталмаған интеграл. f(x) және F(x) функциялары ақырлы немесе ақырсыз Х аралықта анықталған функциялар болсын. Анықтама.Х аралығында дифференциалданатын 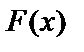 функциясы
функциясы 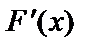 = f(x)теңдігін қанағаттандырса F(x) функциясы f(х) функциясының алғашқы функциясы деп аталады.
= f(x)теңдігін қанағаттандырса F(x) функциясы f(х) функциясының алғашқы функциясы деп аталады.
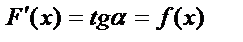
|
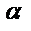
|
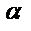
|
| y |
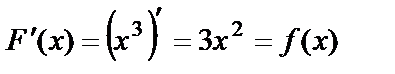
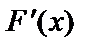 туындының геометриялық мағнасы y=F(x) функциясына х нүктеде жүргізілген жанаманың бұрыштық коэффициенті. Сонда,
туындының геометриялық мағнасы y=F(x) функциясына х нүктеде жүргізілген жанаманың бұрыштық коэффициенті. Сонда, 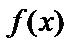 функцияның алғашқы функциясын табу дегеніміз х нүктеде жүргізілген жанамасының бұрыштық коэффициенті сол нүктедегі
функцияның алғашқы функциясын табу дегеніміз х нүктеде жүргізілген жанамасының бұрыштық коэффициенті сол нүктедегі 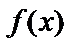 функциясының мәніне тең болатын y=F(x) қисығын табу деген сөз, яғни
функциясының мәніне тең болатын y=F(x) қисығын табу деген сөз, яғни  .
. 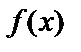 функцияның алғашқы функциясы бірмәнді анықталмаған. Шынында да, мысалдағы f(x)=3x2 функцияларының алғашқы функциялары ретінде мына функцияларды алуымызға болады: x3+1, x3-5, x3+C, мұндағы С-қандай да бір нақты сан (себебі, бұл функциялардың туындысы 3x2 болады). Жалпы жағдайда айтсақ,
функцияның алғашқы функциясы бірмәнді анықталмаған. Шынында да, мысалдағы f(x)=3x2 функцияларының алғашқы функциялары ретінде мына функцияларды алуымызға болады: x3+1, x3-5, x3+C, мұндағы С-қандай да бір нақты сан (себебі, бұл функциялардың туындысы 3x2 болады). Жалпы жағдайда айтсақ, 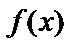 функцияның алғашқы функциясы y=F(x) табылса, онда F(x)+С функциясы да
функцияның алғашқы функциясы y=F(x) табылса, онда F(x)+С функциясы да 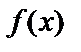 функцияның алғашқы функциясы болады, себебі
функцияның алғашқы функциясы болады, себебі  . Геометриялық тұрғыдан қарастырсақ,
. Геометриялық тұрғыдан қарастырсақ,  шартын қанағаттандыратын бір y=F(x) функция табылса, онда функция графигін Оу осі бойымен С шамаға жылжыту арқылы осы шартты қанағаттандыратын қисықтарды аламыз (бұлай жылжыту бұрыштық коэффициентті өзгертпейді). Анықталмаған интеграл қасиеттері
шартын қанағаттандыратын бір y=F(x) функция табылса, онда функция графигін Оу осі бойымен С шамаға жылжыту арқылы осы шартты қанағаттандыратын қисықтарды аламыз (бұлай жылжыту бұрыштық коэффициентті өзгертпейді). Анықталмаған интеграл қасиеттері
Интеграл анықтамасынан мынадай қасиеттер шығады.
1. 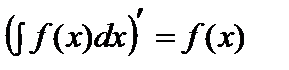 .2.
.2. 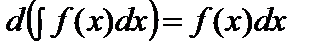 .3.
.3. 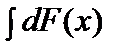 =F(x)+C.4.Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x)+g(x) функциясының да алғашқы функциясы бар болады және
=F(x)+C.4.Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x)+g(x) функциясының да алғашқы функциясы бар болады және 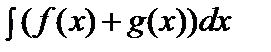
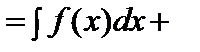
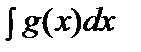 .
.
5. 
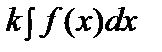 . 6.Егер
. 6.Егер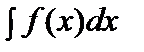 = F(x)+C болса, онда
= F(x)+C болса, онда 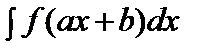 =
=  F(ax+b)+C.
F(ax+b)+C.
7.Егер интеграл астындағы функцияның алымы бөлімнің туындысы болса, онда интеграл бөлімнің абсолют шамасының натурал логарифміне тең, яғни  , мұндағы u=u(x).
, мұндағы u=u(x).
16. Айнымалы алмастыру әдісі. Бөліктеп интегралдау әдісі. Мысалдар. Айнымалыны алмастыру әдісі.I=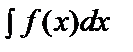 интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және
интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және 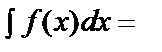
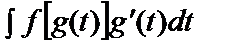 .
.
Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интеграл бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.
а) 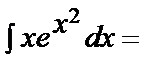
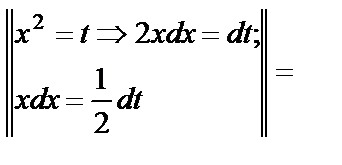

 +С
+С
б) 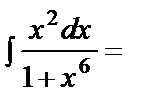

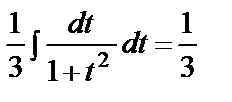 arctgt+C= =
arctgt+C= = 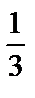 arctgx3+C
arctgx3+C
в) 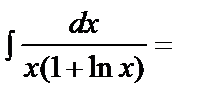
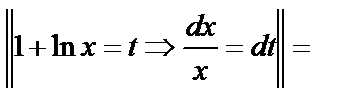
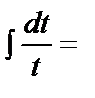 ln|t|+C=ln|1+lnx|+C
ln|t|+C=ln|1+lnx|+C
Бірден интегралдау. Белгілі формулалар көмегімен интегралды бір немесе бірнеше кестелік интегралға келтіруге болатын кезде қолданамыз. Мысалдар қарастырайық.
а)  = =
= = 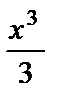 +
+ 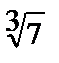
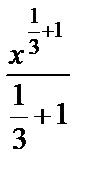 +x+C=
+x+C= 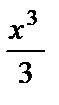 +
+ 
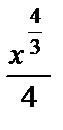 +x+C
+x+C
б) 
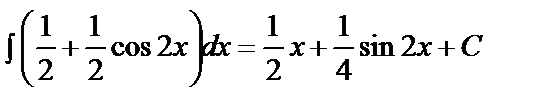 .
.
в) 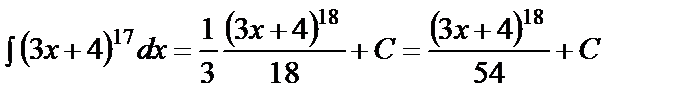
(6-қасиет бойынша есептелді).
г) 
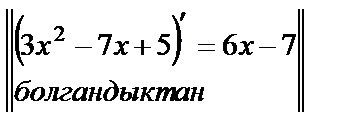 =
= 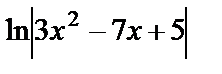 +С.
+С.
Бөліктеп интегралдау әдісі.Бұл әдіс мынадай қатынасқа негізделген:
d(uv) = udv + vdu 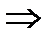 udv = d(uv) – vdu мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ,
udv = d(uv) – vdu мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ,
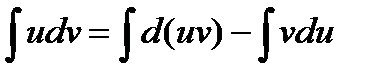 , осыдан
, осыдан 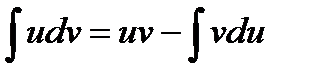 .
.
Бұл әдісті қолданғанда u және v функцияларын 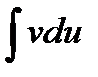 интеграл
интеграл 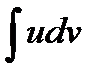 интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық.
интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық.
а) 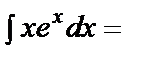
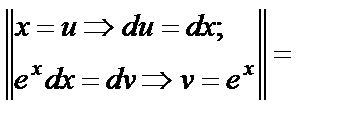
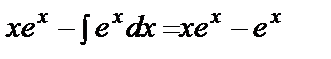 +С =
+С = 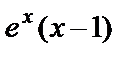 +C.
+C.
б) 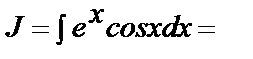
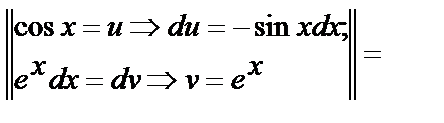
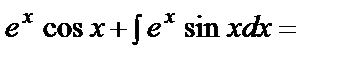
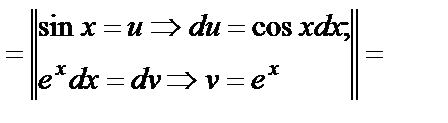
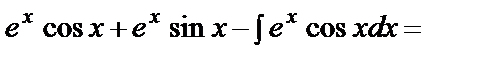
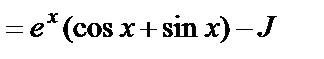 .
.
О= 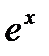 (сщыч+ыштч)-О
(сщыч+ыштч)-О 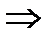 О=
О= 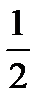
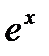 (сщыч+ыштч)+Сю
(сщыч+ыштч)+Сю
Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:
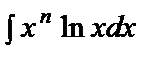 ;
; 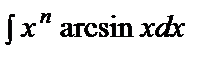 ;
; 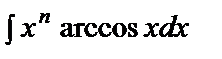 ;
; 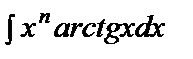 .
.
17. Квадраттық үшмүшелік түріндегі өрнектерді интегралдау. Мына төмендегі интегралдарды табу әдісін қарастырайық 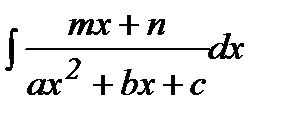 және
және 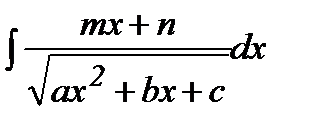 .
.
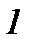 )
)  квадрат үшмүшелігіндегі
квадрат үшмүшелігіндегі 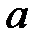 коэффициентін жақша алдына шығарып, одан толық квадратты бөліп аламыз;
коэффициентін жақша алдына шығарып, одан толық квадратты бөліп аламыз;
 ) интегралға
) интегралға 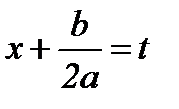 ,
, 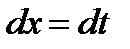 алмастыруын енгіземіз;
алмастыруын енгіземіз;
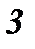 ) Оны екі интегралдың қосындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралға келеді.
) Оны екі интегралдың қосындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралға келеді.
1- мысал. 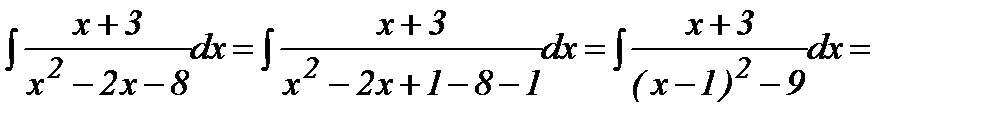

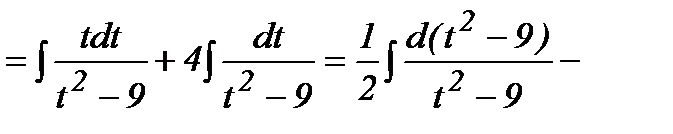



Дата добавления: 2015-01-05; просмотров: 1293; Мы поможем в написании вашей работы!; Нарушение авторских прав |