Бірінші ретті дифференциалдық теңдеулердің негізгі түрлері және оларды шығару тәсілдері. Мысал. 1-ші ретті сызықты біртекті диф.

Бiрiншi реттi дифференциалды теңдеу сызықты деп аталады, егер ол мынадай түрде жазылатын болса:y'+P(x)y=Q(x) 5

Егер (5) теңдеудегі Q(x)=0 болса сызықты теңдеу біртектідеп аталады

y'+P(x)y=0.(Сызықты біртекті дифференциалды теңдеу шешімін бірден алуға болады:

Сонымен, сызықты бiртектi дифференциалды теңдеудiң жалпы шешiмi мынадай: .

Енді (5) теңдеуді шешумен айналысайық. Лагранж әдісі: Бұл әдіс (5) теңдеу шешімін сәйкес біртекті теңдеуінің шешімінен алады. Біртекті теңдеуінің шешіміндегі С шаманы х-тен тәуелді функция деп қарастырамыз: (*).

С(х) функциясын табу үшін у және мәндерін (5) теңдеуге қоямыз. тауып алайық:

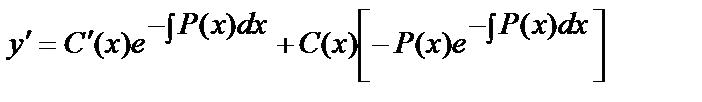.Енді у және мәндерін (5) теңдеуге қоямыз:

; екенін ескеріп, мынаны аламыз:

. Мүшелеп интегралдап, белгісіз С(х) функцияны табамыз:

С(х) функция мәнін (*) теңдеуге қойып (5) сызықты дифференциалды теңдеу шешімін аламыз:

(7)

Мысал. дифференциалды теңдеуді шешу керек.

Шешуі. Теңдеудің екі жағын х-ке бөлсек, сызықты теңдеу аламыз: , мұнда P(x)= , Q(x)=2x³ . Теңдеудің шешімін табу үшін (7) формуланы қолданамыз.

Сонымен, берілген сызықты теңдеу шешімі: .

Анықталған интеграл көмегімен жазық фигураның ауданын, доғаның ұзындығын, айналу денесінің көлемін есептеу Жазық фигураның ауданын табу.

а) функциясы кесіндісінде теріс емес және үзіліссіз болсын. Онда жоғарыдан функциясының графигімен, төменнен өсімен, ал бүйір жақтарынан түзулерімен қоршалған қисық сызықты трапецияның ауданы интегралына тең болады, яғни Егер кесіндісінде болса, онда қисық сызықты трапеция өсінің төменгі жағына орналасқан және болады.

1-мысал. синусоидасымен және осімен шектелген фигураның ауданын табу керек ( ).

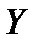
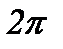
аралығында , ал аралығында 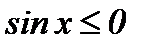болғандықтан, берілген облыстың ауданын табайық

.

б) 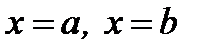түзулерімен және аралығында үзіліссіз (мұндағы ) функциялардың графиктерімен шектелген фигураның ауданы мына формуламен табылады.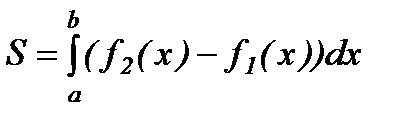

в) Егер кесіндісінде функциясының графигі параметрлік функция түрінде берілсін мұндағы үзіліссіз, ал функциясы кесіндісінде бір сарынды, үзіліссіз дифференциалданатын функция, ал , болса, онда қисық сызықты трапецияның ауданы мына формуламен табылады .

2−мысал. Жарты өстері және болатын эллипстің жоғарғы жағындағы жарты бөлігінің параметрлік теңдеуі былай беріледі: . Егер десек, онда , ал десек тең болады. Сонда эллипстің ауданы былай табылады

.

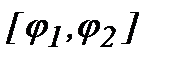Поляр координаттарындағы аудан.Координат төбесінен шығатын сәулелермен және (мұндағы ) және теріс емес функциясының кесіндідегі үзіліссіз графигімен шектелген қисықсызықты үшбұрыштың ауданы мына формуламен есептелінеді:

3-мысал. қисығымен шенелген облыстың ауданын табамыз. Бұл қисық Бернулли лемнискатасы деп аталады.

шартынан интегралдау облысы табылады. Осыдан 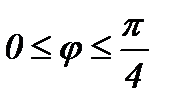үшін бүкіл облыстың -ін құрайды.

.