
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Екі айнымалы функциялар, негізгі ұғымдар. Дербес туындылар және толық дифференциал. Дербес туындының толық диференциялы
Анықтама.z= f(x, y) функциясының дербес өсімшелерінің сәйкес аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған жағдайдағы шегі функцияның дербес туындысы деп аталады және былайша жазылады: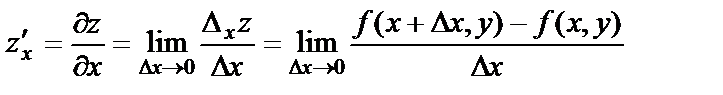
 (5)
(5)
Бұл анықтамадан zх’ туындыны табу үшін у айнымалыны тұрақты деп, ал zy’ туындыны табу үшін х айнымалыны тұрақты деп қарастыру керек. Және де бір айнымалы функция дифференциалынан белгілі дифференциалдаудың барлық ережелері сақталады.
Мысал. 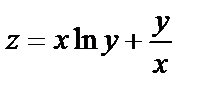 функциясының дербес туындыларын табу керек.
функциясының дербес туындыларын табу керек.
Шешуі. x бойынша дербес туындыны табу үшін у айнымалыны тұрақты деп аламыз, сонда
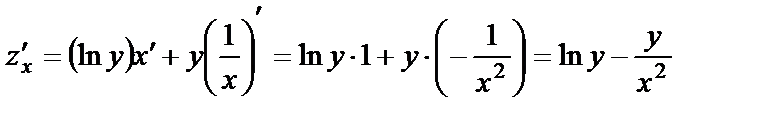 . у бойынша дербес туындыны табу үшін х айнымалыны тұрақты деп аламыз, сонда
. у бойынша дербес туындыны табу үшін х айнымалыны тұрақты деп аламыз, сонда 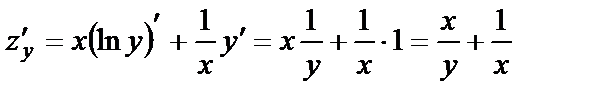 .
.
Анықтама.z= f(x, y) функцияның толық дифференциалы деп осы функцияның дербес туындыларының сәйкес аргумент өсімшелеріне көбейтіндісінің қосындысын айтамыз,
 (*).Егер f(x,y) = x, g(x,y) = y функциялары үшін (*) қатынас бойынша толық дифференциалдарын тапсақ, df = dx=
(*).Егер f(x,y) = x, g(x,y) = y функциялары үшін (*) қатынас бойынша толық дифференциалдарын тапсақ, df = dx=  x, dg = dy=
x, dg = dy=  y болатындығы шығады. Олай болса функцияның толық дифференциалын мына түрде жазуға болады:
y болатындығы шығады. Олай болса функцияның толық дифференциалын мына түрде жазуға болады: 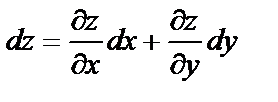 .
.
Дата добавления: 2015-01-05; просмотров: 1858; Мы поможем в написании вашей работы!; Нарушение авторских прав |