исық доғасының ұзындығы

а) Егер қисық декарт координаттар жүйесінде , теңдеуімен берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді: .

б)Егер қисық параметрлік түрде берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді: .

в) Егер қисық сызық полярлық координаталар арқылы берілсе, яғни 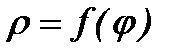( ), онда .

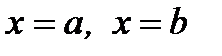Айналу денесінің көлемі.Үзіліссіз сызығымен және түзулерімен шектелген қисық сызықты трапеция өсінен айналуынан пайда болған айналу денесінің көлемі мына формуламен есептелінеді: .

4-мысал. , функциясының графигімен берілген қисық сызықты трапецияның өсінен айналуынан пайда болған дененің көлемін табу керек. Жоғарыдағы формуланы қолданамыз .

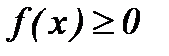Айналу бетінің ауданын табу.Айталық, үзіліссіз дифференциалданатын , ( және ) функциясының графигі өсінен айналсын. Пайда болған айналу бетінің ауданы:

23.Жоғарғы ретті туындылар және дифференциалдар. берілген функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.

Анықтама. Функцияның –ші ретті туындысы деп оның ( -1)-ші туындысының туындысын айтады , =1,2,3,…, егер олар бар болса, онда функциясы -рет дифференциалданатын функция деп аталады.

Мысал. функциясы берілген. Бірінші туындысы 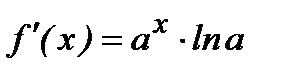, екінші туындысы , үшінші туындысы . Демек, , . Егер және функциялары –рет дифференциалданатын болса, онда ( 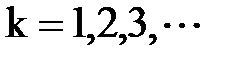), мына ережелер орынды: , .

2. Лейбниц формуласы:

; .

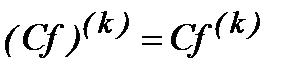Айталық функциясы –рет дифференциалданатын болсын.

Анықтама. Функцияның –ші дифференциалы деп оның ( )–ші ретті дифференциалының дифференциалын айтады: .

Дифференциалды есептеу формулаларын келтірейік:

,

,

,

… … … … … … … … … … … … … … …

. –шы ретті дифференциалдар үшін мына ережелер орынды:

1) , .

2) , .

Ескерту: Жоғарғы ретті дифференциал формасы инвариантты емес.

24.Түзулердің параллельдік және перпендикулярлық шарттары

Егер екі түзу параллель болса, онда =0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k₂ – k₁ = 0. Осыдан екі түзудің параллелдік шарты шығады: k₂ = k₁ , (8) яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда 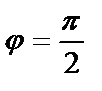болады да, , 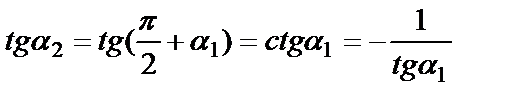. Осыдан екі түзудің перпендикулярлық шарты шығады: k₂ = ,

яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше

25.. 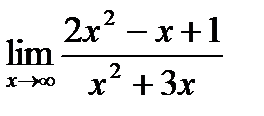шегін есепте.