
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Туынды ұғымы, геометриялық және физикалық мағынасы. Функция туындысы
Көп жағдайда функция мәнін білумен қатар аргументтің өзгерісіне байланысты функцияның өзгеру жылдамдығын білу де маңызды болады.
y=f(x) функциясын қарастырайық (1-сурет). Осы функция  кесіндісінде анықталған және үзіліссіз болсын. Кез келген
кесіндісінде анықталған және үзіліссіз болсын. Кез келген  үшін
үшін  айырма х аргументтің
айырма х аргументтің  нүктесіндегі өсімшесідеп аталады да,
нүктесіндегі өсімшесідеп аталады да,  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,  =
=  x =
x =  +
+ 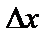 .Ал
.Ал  айырма f(x) функциясының
айырма f(x) функциясының  нүктесіндегі өсімшесідеп аталады да,
нүктесіндегі өсімшесідеп аталады да,  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,  =
= 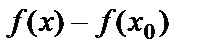 =
=  .
.
2-суретте көрсетілген y=f1(x) және y=f2(x) функцияларды қарастырайық. Аргумент мәні  шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
Аргумент мәні бірдей шамаға өзгерген кездегі функциялардың өзгерістерін салыстыру үшін функцияның өзгеріс жылдамдығы ұғымын енгізеді. Оны орташа жылдамдық дейді де, функция өзгерісінің аргумент өзгерісіне қатынасымен анықтайды:
| Орташа жылдамдық | = | Функция өзгерісі | 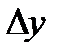
| |
| Аргумент өзгерісі | = | 
|
Орташа жылдамдық х0 нүктесіне ғана қатысты қарастырылмай, аргумент өзгерісінен де байланысты болады. Функция жылдамдығын аргумент өзгерісінен байланыссыз қарастыру үшін функцияның нүктедегі жылдамдығын қарастырады. Функцияның нүктедегі жылдамдығын анықтау үшін х-ті х0 аргументке шексіз жақындатады, немесе  . Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни
. Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни  . Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0нүктедегі өзгеріс жылдамдығын береді. Функцияның х0нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0нүктедегі туындысы деп атайды:
. Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0нүктедегі өзгеріс жылдамдығын береді. Функцияның х0нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0нүктедегі туындысы деп атайды: 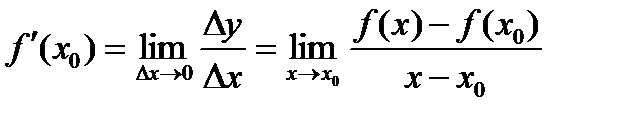 .
.
Анықтама.Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі функция туындысы деп аталады. Әдетте оны 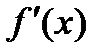 немесе
немесе  деп белгілейді:
деп белгілейді:
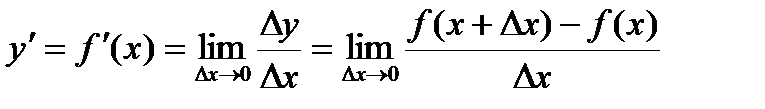
Туындының геометриялық мағынасы: туындысы функциясының графигіне нүктесінде жүргізілген жанаманың бұрыштық коэффициенті болады. Осы жанаманың теңдеуін былай жазады: .Туындының механикалық мағынасы. Егер айнымалысын уақыт деп есептеп, - функциясы дененің жүрген жолын сипаттаса, онда дененің уақытындағы жылдамдығын білдіреді.
Дата добавления: 2015-01-05; просмотров: 1726; Мы поможем в написании вашей работы!; Нарушение авторских прав |