
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция графигінің дөңес және ойыстығы, иілу нүктелері. Асимптоталар.Қисықтың дөңестігі, ойыстығы, иілуі
Анықтама.y=f(x) функция графигі (а,в) интервалының кез келген нүктесінде жүргізілген жанамадан төмен жатса, онда функция дөңес (дөңестігі жоғары қараған) деп, ал жанамадан жоғары жатса, онда функция ойыс (дөңестігі төмен қараған) деп аталады. 3-суретте y=f(x) функциясының графигі  аралығында дөңес болады да, ал
аралығында дөңес болады да, ал  аралығында ойыс болады.Анықтама.Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Суретте қисық бойында жатқан (x0, f(x0)) нүкте графиктің дөңес және ойыс бөліктерін бөліп тұр, яғни ол функцияның иілу нүктесі болады.
аралығында ойыс болады.Анықтама.Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Суретте қисық бойында жатқан (x0, f(x0)) нүкте графиктің дөңес және ойыс бөліктерін бөліп тұр, яғни ол функцияның иілу нүктесі болады.
Енді иілу нүктесін табуға мүмкіндік беретін қажетті және жеткілікті шарттарды қарастырайық. Иілу нүктесі бар болуының қажетті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының (x0, f(x0)) нүктесі иілу нүктесі болса, онда  .Шынында да, (x0, f(x0))иілу нүктесі болғандықтан х0нүктесінің оң және солжағында
.Шынында да, (x0, f(x0))иілу нүктесі болғандықтан х0нүктесінің оң және солжағында  таңбасы түрліше болады. Екінші туындының үзіліссіздігіне байланысты
таңбасы түрліше болады. Екінші туындының үзіліссіздігіне байланысты  болатындығы шығады.
болатындығы шығады.
Анықтама.Екінші туындысы нолге айналатын не болмайтын нүктелер функцияның ІІ-текті күдікті нүктелері деп аталады.Иілу нүктесі бар болуының жеткілікті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының екінші туындысы х аргумент х0 нүкте арқылы өткенде таңбасын өзгертсе, онда (x0, f(x0)) нүктесі функцияның иілу нүктесі болады. Мысал.  (Гаусс қисығы) функциясының иілу нүктелері мен дөңестік аралықтарын тап. Шешуі. 1) Функция бүкіл сан осінде анықталған, яғни D(y)=
(Гаусс қисығы) функциясының иілу нүктелері мен дөңестік аралықтарын тап. Шешуі. 1) Функция бүкіл сан осінде анықталған, яғни D(y)= 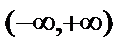 .
.
2) Бірінші және екінші туындыларын табамыз:  ;
;
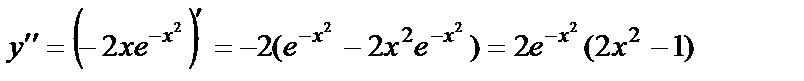 .
.
ІІ-текті күдікті нүктелерін  шартынан табамыз:
шартынан табамыз:  .
.  болғандықтан,
болғандықтан, 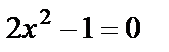 . Осыдан
. Осыдан  және
және  күдікті нүктелер табылады. Осы нүктелер анықталу облысын үш интервалға бөледі:
күдікті нүктелер табылады. Осы нүктелер анықталу облысын үш интервалға бөледі:  ,
,  ,
,  .
.
Осы интервалдардағы екінші туынды таңбасын анықтаймыз (4-сурет):
у
   
ойыс дөңес ойыс
4-сурет 5-сурет |
Сонымен функция графигі  және
және  аралықтарда ойыс, ал
аралықтарда ойыс, ал  аралықта дөңес болады екен. Екінші ретті
аралықта дөңес болады екен. Екінші ретті  туынды
туынды  нүктелерден өткенде таңбасын өзгертетіндіктен, бұл нүктелер функцияның иілу нүктелері болады. Функция графигі 5-суретте кескінделген.
нүктелерден өткенде таңбасын өзгертетіндіктен, бұл нүктелер функцияның иілу нүктелері болады. Функция графигі 5-суретте кескінделген.
Дата добавления: 2015-01-05; просмотров: 1965; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 + - +
+ - + х
х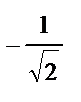 0
0 