
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анықталған интеграл қасиеттері.
1. Тұрақтыны шек таңбасы алдына шығаруға болады: 
 .
.
1. Екі функцияның алгебралық қосындысының интегралы сол функциялар интегралдарының алгебралық қосындысына тең болады: 
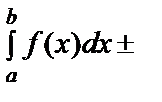
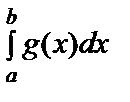 .
.
3Интеграл шектерінің орындарын ауыстырғанда интеграл таңбасы қарама-қарсыға өзгереді: 
 . Интеграл шектері бірдей болғанда интеграл мәні нолге тең:
. Интеграл шектері бірдей болғанда интеграл мәні нолге тең:  .
.
Tuth  ,jkcf? jylf m(b-a)<
,jkcf? jylf m(b-a)<  <M(b-a)/ Егер с нүктесі [a;b] кесіндісінде жатқан нүкте болса, онда
<M(b-a)/ Егер с нүктесі [a;b] кесіндісінде жатқан нүкте болса, онда 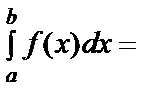

 .
.
Орта мән туралы теорема. y=f(x) функциясы [a;b] кесіндісінде үзіліссіз функция болса, онда қандай да бір с  [a;b] нүкте табылады да мына теңдік орындалады:
[a;b] нүкте табылады да мына теңдік орындалады:  (b-a)f(c).
(b-a)f(c).
Егер y=f(x) функциясы жұп болса, онда  2
2  .
.
Егер y=f(x) функциясы тақ болса, онда  0.
0.
2. Ньютон-Лейбниц формуласы. 
 F(b) – F(a),мұндағы
F(b) – F(a),мұндағы 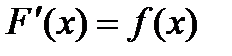 .
.
Анықталған интегралдағы бөліктеп интегралдау: 

 .
.
Анықталған интегралдағы айнымалыны алмастыру:


 .
.
4.Меншіксіз интеграл. Егер y=f(x) функциясы  аралығында үзіліссіз болса, онда мына шекті
аралығында үзіліссіз болса, онда мына шекті  жоғары шегі шексіз меншіксіз интеграл дейді және былай жазады:
жоғары шегі шексіз меншіксіз интеграл дейді және былай жазады:

 .
.
Теңдіктің оң жағындағы шек ақырлы болса меншіксіз интеграл жинақталады деп, ал шек ақырсыз немесе болмаса меншіксіз интеграл жинақталмайды дейді. Осыған ұқсас мынадай меншіксіз интегралдар анықталады:

 ,
, 
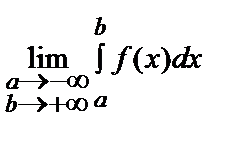 .
.
19. Анықталған интегралда айнымалыны алмастыру және бөліктеп интегралдау әдісі. Мысалдар..Айнымалыны алмастыру әдісі.I=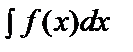 интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және
интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және 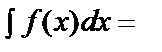
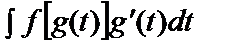 .
.
Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интеграл бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.
а) 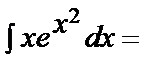
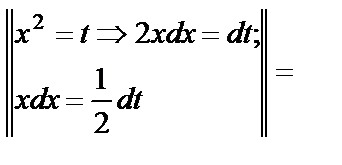

 +С
+С
б) 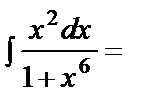

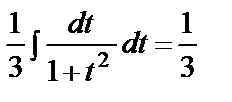 arctgt+C= =
arctgt+C= = 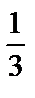 arctgx3+C
arctgx3+C
в) 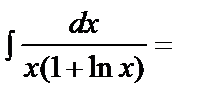
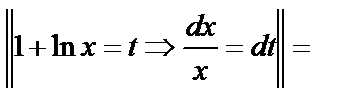
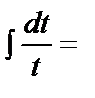 ln|t|+C=ln|1+lnx|+C
ln|t|+C=ln|1+lnx|+C
Бөліктеп интегралдау әдісі.Бұл әдіс мынадай қатынасқа негізделген:
d(uv) = udv + vdu  udv = d(uv) – vdu мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ,
udv = d(uv) – vdu мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ,
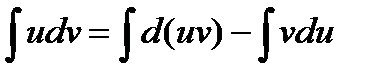 , осыдан
, осыдан 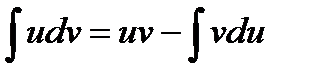 .
.
Бұл әдісті қолданғанда u және v функцияларын 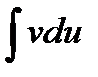 интеграл
интеграл 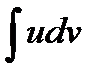 интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық.
интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық.
а) 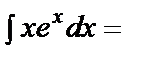
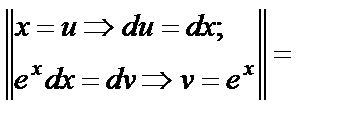
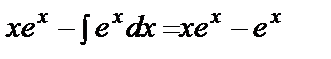 +С =
+С = 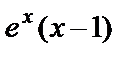 +C.
+C.
б) 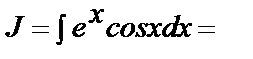
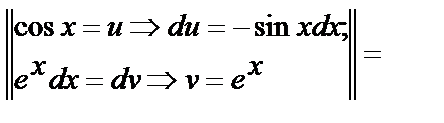
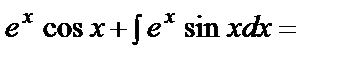
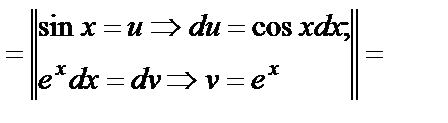
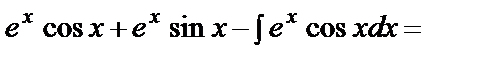
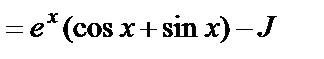 .
.
О= 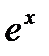 (сщыч+ыштч)-О
(сщыч+ыштч)-О 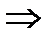 О=
О= 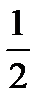
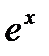 (сщыч+ыштч)+Сю
(сщыч+ыштч)+Сю
Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:
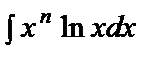 ;
; 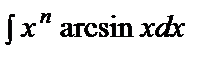 ;
; 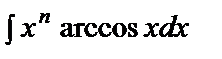 ;
; 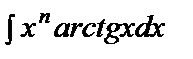 .
.
Дата добавления: 2015-01-05; просмотров: 1258; Мы поможем в написании вашей работы!; Нарушение авторских прав |