
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Москва 2005
Явление–философская категория, означающая то или иное обнаружение предмета, внешние формы его существования; сущность выражает внутреннее содержание предмета в единстве всех связей и отношений. В познании сущность и явление выступают как ступени познания предмета (от явления к сущности).
Я-концепция – система представлений о самом себе, своей роли в окружающем мире, о мире в целом.
Московский институт управления
МАТЕМАТИКА
Методическое пособие
Для заочного выполнения
Контрольных заданий.
I часть.
Исполнитель:
Кандидат технических наук Дубчак В.С.
Доцент кафедры гуманитарных
И естественных наук
Москва 2005
Данное «Методическое пособие для заочного выполнения Контрольных заданий» составлено в соответствии с «Программой» по предмету «Математика» для экономических специальностей и «Календарным планом», принятым на заседании кафедры 28.08.2004г.
Содержание заданий:
Задание №1.
- Матрицы. Определители матриц.
- Системы линейных алгебраических уравнений и методы их составления и решения.
- Уравнения прямой.
- Пределы функций. Правило Лопиталя. Асимптоты функций.
- Дифференцирование простых и сложных функций.
Задание №2.
- Дифференцирование взаимосвязанных функций двух переменных.
- Частные производные. Локальный, общий, условный экстремум.
- Приложения производных для исследования функций одного и двух переменных на оптимум.
Задание №3.
- Неопределенный интеграл.
- Определённый интеграл и его приложение.
- Дифференциальные уравнения первого и второго порядка.
- Приложение к задачам экономики.
- Метод наименьших квадратов и применение его для аналитической интерпретации статистических данных.
Задание №4.
- Эластичность функций
- Исследование операций
- Линейное программирование. Графический метод.
- Симплекс-метод для многих параметров
- Транспортная задача в экономике
Задания выдаются преподавателем из специального дополнения к пособию,
которое содержит исходные данные для соответствующих вариантов. В пособии приведены типовые примеры решений задач.
Цель преподавания математического минимума в экономическом ВУЗе – познакомить студентов с математическим аппаратом, необходимым для анализа процессов, имеющих статический (балансный), динамический (дифференцированный во времени) и стохастический (случайный) характер. При решении практических задач на базе теоретических знаний синтезируются оптимальные и объективные результаты. Умение математического моделирования условия задачи и определение наилучшего результата из множества позволяет с применением ЭВМ готовить проекты и решения на современном уровне и без больших материальных затрат.
Специфика заочной формы обучения состоит в самостоятельном изучении литературы по математическим методам решения экономических задач. Пособие, максимально охватывая обязательные вопросы программы, позволяет помочь студентам сократить время на поиски соответствующего материала, который здесь сконцентрирован из различных разрозненных источников. Кроме того, по каждой задаче пособие содержит образец решения.
Правила выполнения контрольных заданий:
- Контрольную работу следует выполнять в тетради, отдельной для каждого задания.
- Каждая задача должна иметь дробный номер. Например №3/5 – третье задание; пятая задача.
- Перед решением каждой задачи надо выписать полностью ее условие
- Решение задачи следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи и графики.
- Там, где возможно, необходимо проверять полученные результаты.
- Работа выполняется чернилами (пастой) любого цвета, кроме красного, оставляя поля шириной 4см для замечаний рецензента.
- После получения прорецензированной работы студент должен исправить все отмеченные недочеты, ошибки и выполнить рекомендации
- Каждая работа оценивается отдельно. Допуск к экзамену возможен только после выполнения (оценки) всех четырёх работ со своим сочетанием вариантов задач.
- Титульный лист работы должен содержать необходимые визитные данные:
группа, фамилия, имя и отчество, учетный номер (шифр) студента, номер контрольной работы, название дисциплины, дату сдачи (отсылки) работы, адрес студента. В конце работы желательно указать список использованной литературы.
Задание №1
Задача № 1/1.
Предприятие выпускает три вида продукции, используя сырье трех типов. Необходимые характеристики производства указаны в следующей таблице:
| Виды сырья | Нормы расхода сырья на единицу продукции | Запасы сырья | ||
| 1 | 2 | 3 | ||
| 6 3 | 4 4 | 5 2 | ||
| 4 1 | 3 2 | 1 1 | ||
| 5 5 | 2 1 | 3 3 |
Определить объем выпуска продукции каждого вида при условии полного использования сырья.
Примечание: составленную систему линейных алгебраических уравнений (СЛАУ) решить тремя методами и провести проверку результатов.
Решение: Обозначим искомые объемы соответственно X1, Х2, Х3.
Так как в данной задаче исходные данные позволяют составить тривиальную систему (количество неизвестных равно количеству уравнений), то результат получаем окончательный и в единственном виде. СЛАУ представляет собой равенства запасов сырья соответствующим суммам произведений норм расхода на соответствующие объемы продукции:
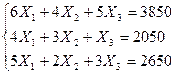
Такая система содержит т.н. балансные уравнения.
Решение методом Крамера (определители матриц)

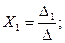
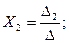
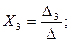
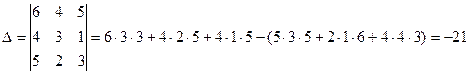
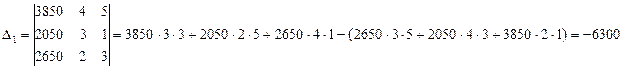
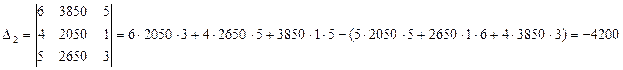
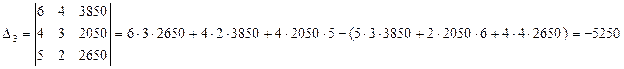
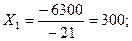
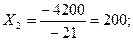

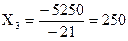
Проверим подстановкой во второе уравнение как наиболее простое в цифрах:
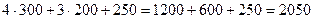
Получено тождество, что свидетельствует о верном решении.
Решение методом Гаусса (последовательное исключение неизвестных).
Расширенная матрица
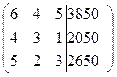
Умножим первую строку сначала на 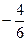 и прибавим ко второй, затем на
и прибавим ко второй, затем на 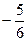 и прибавим к третьей. Так формируются новые строки – вторая и третья с нулевыми коэффициентами при Х1. Тем самым понижается порядок матрицы от n=3 до n=2, где остались Х2 и Х3 .
и прибавим к третьей. Так формируются новые строки – вторая и третья с нулевыми коэффициентами при Х1. Тем самым понижается порядок матрицы от n=3 до n=2, где остались Х2 и Х3 .
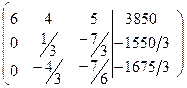 - матрица I шага.
- матрица I шага.
Умножим вторую строку полученной матрицы на 4 и прибавим ее к третьей строке, обнуляя коэффициент при Х2 .
 - матрица II шага.
- матрица II шага.
Последний вид расширенной матрицы является конечным этапом прямого хода, на основании которого составим систему уравнений для обратного хода
(1) 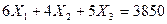
(2) 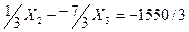
(3) 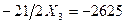
Из (3) → 
Из (2) → 
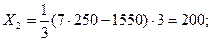
Из (1) → 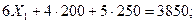

Получаем тот же результат, что и I методом.
Решение методом обратной матрицы
Главный определитель системы
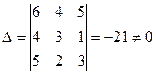 , значит обратная матрица существует.
, значит обратная матрица существует.
Находим алгебраические дополнения элементов матрицы через соответствующие миноры:
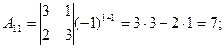
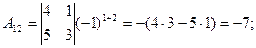

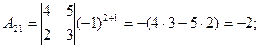
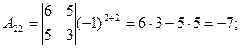
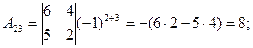
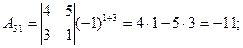
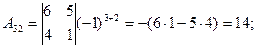
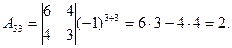
Из алгебраических дополнений составим матрицу 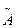 и транспонируем ее
и транспонируем ее 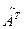 .
.
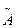 =
= 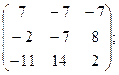
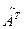 =
= 
Обратная матрица
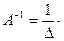
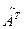 =
= 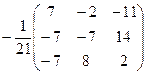
Матрицу – столбец неизвестных Х получим как произведение обратной матрицы на матрицу – столбец свободных членов
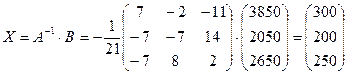
Следовательно
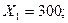
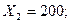
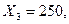 т.е. результат тот же, что при решении предыдущими методами.
т.е. результат тот же, что при решении предыдущими методами.
Дата добавления: 2015-01-05; просмотров: 273; Мы поможем в написании вашей работы!; Нарушение авторских прав |