Дифференциальные уравнения.

А) Найти динамику цены P(t) на товар по заданным из статистики соотношениям, описывающим прогноз спроса D(t) и предложения S(t) при начальных условиях P(0)=1.1;3 P’(0)= -17; 1,5

D(t)=5p”+10p’+18p+8; S(t)=4p”-3p’-12p+11;

D(t)=3p”+3p’+8p-5; S(t)=2p”-1p’+5p+7;

Решение:

Динамика установления равновесия цены определяется равенством D(t)=S(t), т.е. 5p”+10p’+18p+8=4p”-3p’-12p+11;

p”+13p’+30p=3 – линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.

1) Найдем общее решение соответствующего однородного уравнения:

p”+13p’+30p=0, т.е. P_0P

Характеристическое уравнение

k²+13k+30=0;

2) Частное решение неоднородного уравнения

P_4P =A=const; p’=p”=0;

P”+13p’+30p=3; 0+0+30A=3; A=3/30=0.1

3)Полное решение P= P_0P+P_4P= +0.1 получим после определения значений произвольных постоянных С₁ и С₂ интегрирования, используя начальные условия.

При t = 0

=

= ;

;

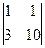б) Решить: линейное неоднородное дифференциальное уравнение

Решение.

1) ; ;

; ;

2) ; ; ;

; ;