
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №4/2 Симплекс-метод
Торговое предприятие, располагающее материально-денежными ресурсами реализует три группы товаров. Плановые нормативы затрат ресурсов на единицу товарооборота (  ), прибыль от продажи товаров на единицу товарооборота по статданным (
), прибыль от продажи товаров на единицу товарооборота по статданным (  ), а также объемы ограничений ресурсов (
), а также объемы ограничений ресурсов (  ) сведены в таблицу.
) сведены в таблицу.
Определить объем и структуру товарооборота так, чтобы прибыль торговогопредприятия в целом была бы максимальной (числа в задаче в условных единицах в соответствии с размерностями нормативных данных).
| X1 | X2 | X3 | |||||
| № п/п | Виды материальных ресурсов | Единицы измерения | Норма затрат ресурсов на ед.т/о,тыс.руб. | Объем ресурсов (bi) | |||
| I гр.(ai1) | II гр.(ai2) | III гр.(ai3) | |||||
| Рабочее время продавцов | чел/час | 4 2 | 2 1 | 6 3 | |||
| Площадь торговых залов | 
| 2 1 | 4 2 | 3 1 | |||
| Площадь складских помещений | 
| 6 6 | 8 4 | 0 2 | |||
| Единичная прибыль (Cj) | тыс. руб. | 2 2 | 3 2 | 2 3 | |||
Запишем математическую модель задачи
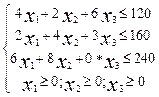
Целевой функционал
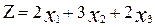
нужно максимизировать.
1)Составление первого опорного плана.
Применим “размножение неизвестных”, т. е., чтобы из неравенств получить систему уравнений, дополним каждое из них неотрицательными вспомогательными неизвестными той же размерности, что и члены уравнений.
Такой вид называется каноническим.
Выразим дополнительные неизвестные через основные (базисные)
х4=120-(4х1+2х2+6х3)
х5=160-(2х1+4х2+3х3)
х6=240-(6х1+8х2)
В начальной (исходной) позиции целевой функционал запишем в виде
z =0-(2х1+3х2+2х3)
Соответственно Ι симплексная таблица (ΙСТ) будет:
| Дополнительные переменные | При нулевых значениях х1,х2,х3 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | θ |
| Х4 | ||||||||
| Х5 | ||||||||
| Х6 | 30 
| |||||||
| Z | -2 | -3 | -2 |
1 CТ
2) Проверка плана на оптимальность. План будет оптимальный тогда, когда индексная строка £ „перестанет” содержать отрицательные коэффициенты. Сейчас план не оптимальный, т.к. коэффициенты < 0
3) Определение „направляющих” столбца и строки.
Наиболее „тяжёлым” является коэффициент (-3) как наибольший по абсолютной
величине. По этой прчине Х2 как принадлежность «указующего» столбца далее перейдет в иной разряд и заменит одну из искомых новых переменных. А для определения, какую переменную она заменит делим свободные члены на соответствующие коэффициенты «указующего» столбца: и заносим в служебный столбец θ (см 1 СТ)
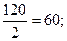
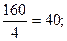

«Указующая» строка там, где θmin=30, что соответствует Х6.
Т.о. в новом опорном плане II шага (2 СТ) Х6 заменяем на Х2
4) Определение нового опорного плана 2 СТ Для формирования 2 СТ применяется метод Жордана-Гауса, который состоит в следующем:
Вместо строки Х6 записывается пересчитанная строка Х2 путем деления всех элементов строки Х6 таблицы 1 СТ на цифру в перекрестии Х6 и Х2, т.е. на 8:

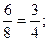
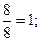
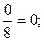
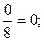
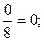
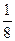
А в остальных клетках столбца Х2 «накапливаем» нули аналогично тому, как это делалось при решении СЛАУ методом Гаусса (см. таблицу 2 СТ).
2 СТ
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Ө | ||
| Х4 | 5/2 | -1/4 | ||||||
| Х5 | -1 | -1/2 | 40/3 | |||||
| Х2 | ¾ | 1/8 | бесконечность | |||||
| Z | 1/4 | -2 | 3/8 |
Так, например, для получения О на пересечении строки Х4 со столбцом Х2 используем полученную 1 таблицы 2 СТ, для чего все элементы новой строки Х2 табл. 2 СТ множим на коэффициент пересечения строки Х4 и столбца Х2 таблицы 1 СТ, но с противоположным знаком (-2) и складываем с элементами строки Х4 табл. 1СТ, а результат заносим в строку Х4 таблицы 2СТ, а именно:
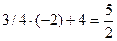 ;
; 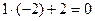 ;
; 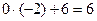 ;
;
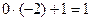 ; 0(-2)+0=0;
; 0(-2)+0=0; 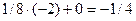
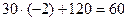
Аналогично для строки Х5 будет множитель(-4)
 ;
;  ;
; 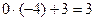 ;
;
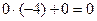 ;
; 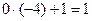 ;
; 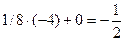 .
.

Аналогично для строки Z будет множитель (+3)
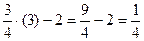 ;
; 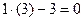 ;
; 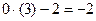 ;
;
 ;
;  ;
; 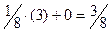 ;
; 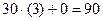
5. В результате видим, что план таблицы 2СТ все же не оптимальный, т.к. в строке Z коэффициент при Х3 меньше 0 (-2).
Поэтому по тому же алгоритму формируем опорный план III
шага (3СТ)
Теперь «направляющим» столбцом является Х3 (см. таблицу 2СТ)
Пересчитываем столбец q
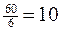 ;
; 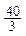 ;
; 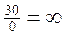
Т.о. «указующей» строкой будет Х4, т.к.
qmin 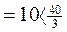
Аналогично заменяем Х4 на Х3 и делим все ее элементы на цифру «указующих» столбца Х3 и строки Х4, т.е. на 6.
 ;
; 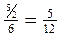 ;
; 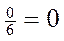 ;
; 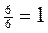 ;
; 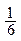 ;
;  ;
; 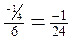
«Накапливаем» нули для таблицы 3СТ :
строка Х5 (множитель(-3))
 ;
; 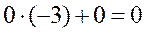 ;
; 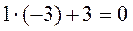 ;
; 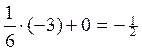 ;
;  ;
;  ;
; 
Строка Z будет множитель (2)
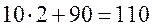 ;
; 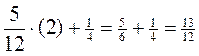
 ;
; 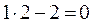 ;
;  ;
;
 ;
; 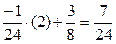
3 СТ
| X1 | X2 | X3 | X4 | X5 | X6 | ||
| X3 X5 X2 | 5/12 -9/4 3/4 | 1/6 -1/2 | -1/24 -3/8 1/8 | ||||
| Y | 13/12 | 1/3 | 7/24 |
3cт соответствует оптимально приемлемому плану, т.к. все коэффициенты в индексной строке Y больше нуля (положительные).
Оптимальный план:
Х=(0; 30; 10; 0; 10; 0) и Y(х)=110 тыс. рублей.
Следовательно вывод:
Для получения максимальной прибыли в размере 110 тыс. руб. предприятию необходимо продавать товары 2 группы на 30 тыс. руб., 3 группы на 10 тыс. руб., а 1 группы продавать не рентабельно. Кроме того, ресурсы Ⅱ вида (площадь торговых залов) недоиспользованы на 10 м. кв. (Х5=10).
Остальные ресурсы используются полностью (Х4=Х6=0).
Задача № 4/3.
Дата добавления: 2015-01-05; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |